![]()
8 동적 계획법 8.1 도입 동적 계획법(dynamic programming)이라는 말은 최적화 문제를 연구하는 수학 이론에서 왔으며, 우리가 전산학 전반에서 일반적으로 사용하는 동적(dynamic), 혹은 프로그래밍(programming)이라는 단어와는 아무런 관련이 없다. 중복되는 부분 문제 동적 계획법은 큰 의미에서 분할 정복과 같은 접근 방식을 의미한다. 동적 계획법을 사용하는 알고리즘들 또한 처음 주어진 문제를 더 작은 문제들로 나눈 뒤 각 조각의 답을 계산하고, 이 답들로부터 원래 문제에 대한 답을 계산해 내기 때문이다. 동적 계획법과 분할 정복의 차이가 발생하는 부분은 문제를 나누는 방식이다. 동적 계획법에서 어떤 부분 문제는 두 개 이상의 문제를 푸는데 사용될 수 있기 때문에, 이 문제의 ..
![]()
7 분할 정복 7.1 분할 정복 분할 정복(Divide & Conquer)은 가장 유명한 알고리즘 디자인 패러다임으로, 각개 격파라는 말로 간단히 설명할 수 있다. 분할 정복 패러다임을 차용한 알고리즘들은 주어진 문제를 둘 이상의 부분 문제로 나눈 뒤 각 문제에 대한 답을 재귀 호출을 이용해 계산하고, 각 부분 문제의 답으로부터 전체 문제의 답을 계산해 낸다. 분할 정복이 일반적인 재귀 호출과 다른 점은 문제를 한 조각과 나머지 전체로 나누는 대신 거의 같은 크기의 부분 문제로 나누는 것이다. 이 차이점이 아래 그림이다. 그림 (a)는 항상 문제를 한 조각과 나머지로 쪼개는 일반적인 재귀 호출 알고리즘을 보여주고, 그림 (b)는 항상 문제를 절반씩으로 나누는 분할 정복 알고리즘을 보여준다. 분할 정복을 ..
![]()
06 무식하게 풀기 6.1 도입 흔히 전산학에서 무식하게 푼다(brute-force)는 말은 컴퓨터의 빠른 계산 능력을 이용해 가능한 경우의 수를 일일이 나열하면서 답을 찾는 방법을 의미한다. 이렇게 가능한 방법을 전부 만들어 보는 알고리즘들을 가리켜 흔히 완전탐색(exhaustive search)이라고 부른다. 얼핏 보면 이런 것을 언급할 가치가 있나 싶을 정도로 간단한 방법이지만, 완전탐색은 사실 컴퓨터의 장점을 가장 잘 이용하는 방법이다. 컴퓨터의 최대 장점은 속도가 빠르다는 것이기 때문이다. 6.2 재귀 호출과 완전 탐색 재귀 호출 재귀 함수란 자신이 수행할 작업을 유사한 형태의 여러 조각으로 쪼갠 뒤 그 중 한 조각을 수행하고, 나머지를 자기 자신을 호출해 실행하는 함수를 가리킨다. 예를 들면 ..
![]()
02 알고리즘 분석 (04 ~ 05) 04 알고리즘 시간 복잡도 분석 4.1 도입 두 알고리즘의 속도를 비교하는 가장 직관적인 방법은 각각을 프로그램으로 구현한 뒤 같은 입력에 대해 두 프로그램의 수행 시간을 측정하는 것이다. 하지만 프로그램의 실행 시간은 알고리즘의 속도를 일반적으로 이야기하는 기준이 되기에는 부적합하다. 가장 큰 이유는 프로그램의 수행 시간은 사용한 프로그래밍 언어, 하드웨어는 물론이고 운영체제, 컴파일러까지 수 많은 요소에 의해 바뀔 수 있기 때문이다. 두 번째 이유는 실제 수행 시간이 다양한 입력에 대한 실행 시간을 반영하지 못하기 때문이다. 알고리즘의 수행 시간을 지배하는 것은 반복문이다. 입력의 크기가 작을 때는 반복외의 다른 부분들이 갖는 비중이 클 수가 있지만, 입력의 크기..
![]()
이번 포스팅에서는 킥스타트 2020 Round D에 대한 문제 풀이를 공유하고자 한다. 1. Record Breaker 배열을 반복하면서 조건문을 통해 카운팅을 하면 쉽게 풀 수 있는 문제이다. 시간복잡도는 O(N) 2. Alien Piano 이 문제는 Greedy 알고리즘을 사용해서 풀었다. 먼저 배열을 통해 각각의 note의 pitch를 받아서 채워준다. 이 때 연속해서 같은 값이 나오게 되면 같은 alien piano key를 사용하게 되므로 배열에 넣어주지 않아도 된다. 이렇게 배열을 넣어 주었을 때 만약 다음과 같이 배열이 생겼다고 가정해 보자. 이 때는 연속해서 두 숫자가 같은 경우는 존재하지 않을 것이다. [1, 8, 9, 7, 6, 5, 4, 3, 2, 1, 3, 2, 1, 3, 5, 7]..
![]()
이번 포스팅에서는 킥스타트 2020 Round C에 대한 문제 풀이를 공유하고자 한다. 1. Countdown 간단한 배열 문제이다. 배열의 반복문을 돌면서 주어진 숫자부터 시작되는 카운트 다운이 총 몇 개인지를 세어 주면 된다. 한 번 배열을 순환해서 답을 구할 수 있기 때문에 시간복잡도는 O(N). 2. Stable Wall 그래프 개념을 가지고 풀어야 하는 조금 까다로운 문제이다. 나의 경우 다른 사람의 풀이를 조금 참고하면서 풀었다. 문제를 이해하는 것 부터 쉽지가 않았던 것 같다. 위상 정렬(topological sort)과 DFS를 사용하였다. N개의 폴리노미노(polynomino)가 있고 이것들이 stable한 경우, 즉 각각의 폴리노미노가 바닥에 붙어 있거나, 다른 폴리노미노 위에 올라타 ..
![]()
킥스타트 2020 라운드 B 문제 풀이를 해 보도록 한다. 내년 2021 킥스타트나 코드잼을 준비하시는 분들, 또는 알고리즘 공부를 하시는 분들에게 많은 도움이 되길 바란다. 1. Bike Tour 기초적인 탐색 문제이다. 전체 체크포인트 N개를 배열에 저장한 후 처음부터 끝까지 탐색하며 peak가 몇 개인지 파악하면 된다. 시간복잡도는 O(N). import java.io.*; import java.util.*; public class KickStart_2020B_1 { public static void main(String[] args) throws IOException { BufferedReader br = new BufferedReader(new InputStreamReader(System.in)..
![]()
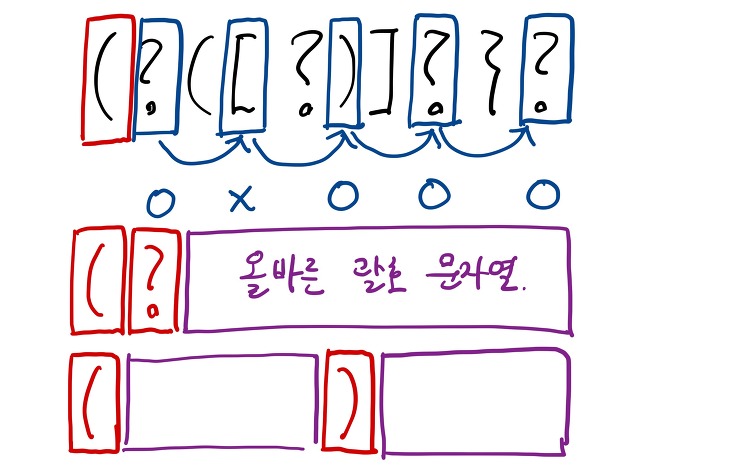
오늘은 백준 3012번 문제를 풀어보려고 한다. 이 문제는 07/08 크로아티아 정보올림피아드 기출문제이다. https://www.acmicpc.net/problem/3012 3012번: 올바른 괄호 문자열 예제 1의 경우 다음이 가능하다. ({([()])}), ()([()]{}), ([([])]{}) www.acmicpc.net 크로아티아 정보올림피아드 기출 문제여서 그런지 문제에 대한 아이디어가 쉽게 떠오르지는 않았던 것 같다. (난이도도 심지어 플레티넘 3 ㄷㄷ...) 처음에는 ? 각각에 들어갈 수 있는 문자 "{", "[", "(" 등을 찾아서 경우의 수를 생각해 주어야 하나? 라고도 떠올려 봤는데 너무 생각해 주어야 할 케이스가 많았고 이 방법은 맞지 않다는 것을 깨달았다. 결국 DP를 통해 한..