오늘 살펴볼 문제는 백준 3176번 '도로 네트워크' 라는 문제이다.
https://www.acmicpc.net/problem/3176
3176번: 도로 네트워크
문제 N개의 도시와 그 도시를 연결하는 N-1개의 도로로 이루어진 도로 네트워크가 있다. 모든 도시의 쌍에는 그 도시를 연결하는 유일한 경로가 있고, 각 도로의 길이는 입력으로 주어진다. 총 K
www.acmicpc.net

이 문제는 꽤 어렵다. https://solved.ac/ 라는 알고리즘 문제 난이도 측정 사이트에서는 이 문제를 플레티넘 4 레벨로 분류했다. 플레티넘 레벨은 상당수가 쉽게 해결책을 찾기 어려운 고난이도 문제이다.(나에게는) 이 문제도 그래서 사실 풀다가 다른 사람의 소스를 어느 정도 참고하였고, 천천히 상세하게 풀이를 정리하면서 공부하는 목적으로 적어 보려고 한다.
이 문제는 LCA 알고리즘을 알아야 풀 수 있는 문제이다. 따라서 먼저 이 알고리즘에 대해 간단하게 설명을 해 보려고 한다.
LCA(Lowest Common Ancestor) 알고리즘, 우리말로 하면 최소 공통 조상 알고리즘 정도가 되는데 말 그대로 트리 구조에서 두 노드가 주어졌을 때 가장 가까운 공통 조상을 찾는 알고리즘이다.

이와 같은 트리가 하나 있다고 가정을 해 보자. 여기서 LCA(4,12)는 무엇일까?
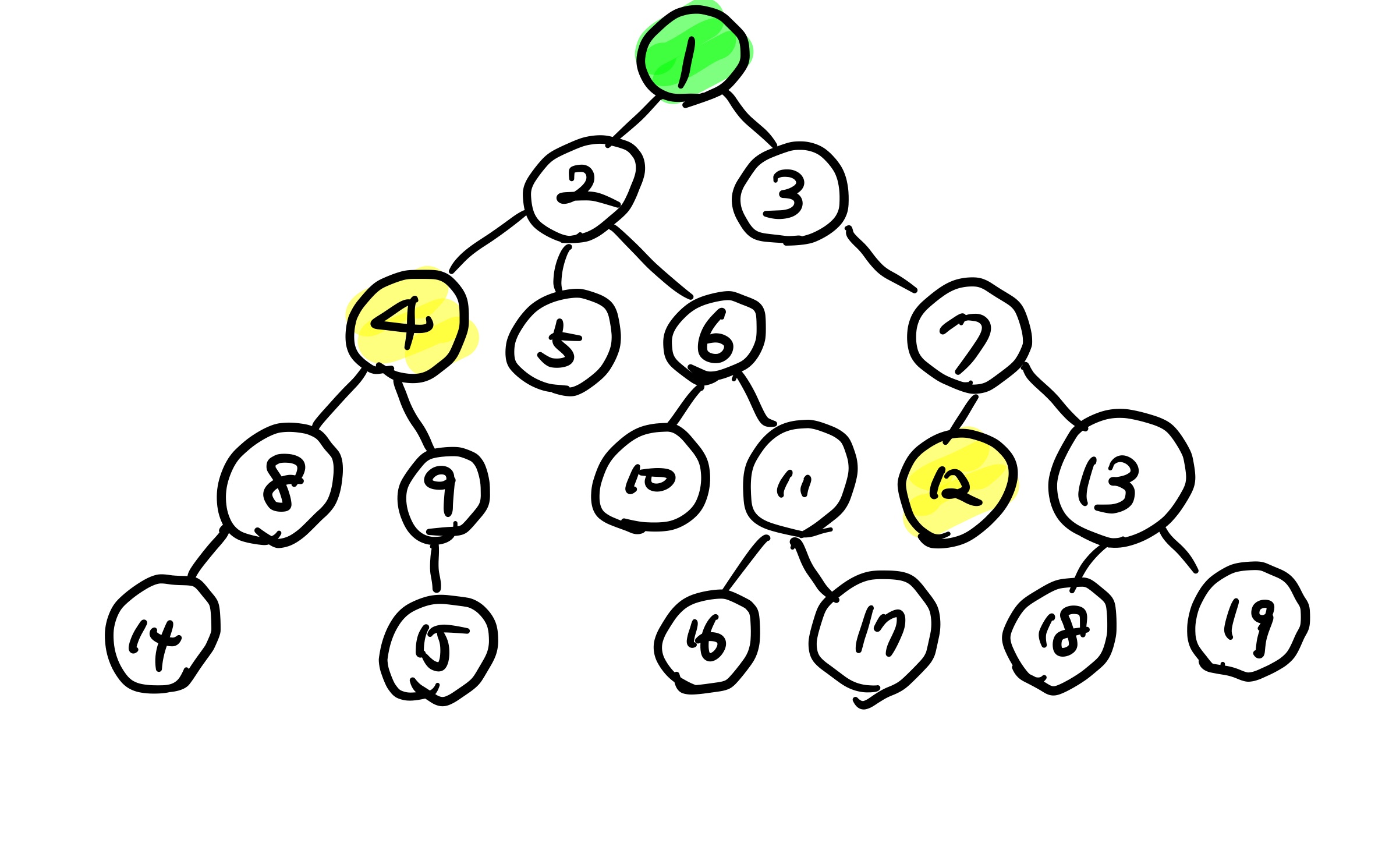
4와 12의 공통 조상은 1임을 그림에서 쉽게 알 수 있다. 하지만 만약 트리가 수백 개 또는 그 이상이라면, 이렇게 그림으로 보고 알기는 쉽지 않다. 따라서 LCA 알고리즘이 어떤 식으로 돌아가는 지를 알 필요가 있다.
LCA 알고리즘의 해석에는 여러가지 방법이 있지만, 이번 포스팅에서는 DP(동적 계획법)을 가지고 설명해 보려고 한다. 동적 계획법은 이전 포스팅에 어떤 방법인지 설명한 바가 있다. 간단하게 설명하면 값들을 메모해서 기억한 뒤 필요할 때 바로바로 꺼내 쓰는 방법이다.
각각의 노드의 깊이와 해당 노드에서 2^N(N은 0 이상의 정수)번째 부모의 값을 메모해 놓는다. 모든 부모를 다 저장하면 시간이 너무 오래 걸리고, 메모리 공간을 많이 차지하기 때문에 2^N 번째 부모 노드값만 저장하는 것이다.
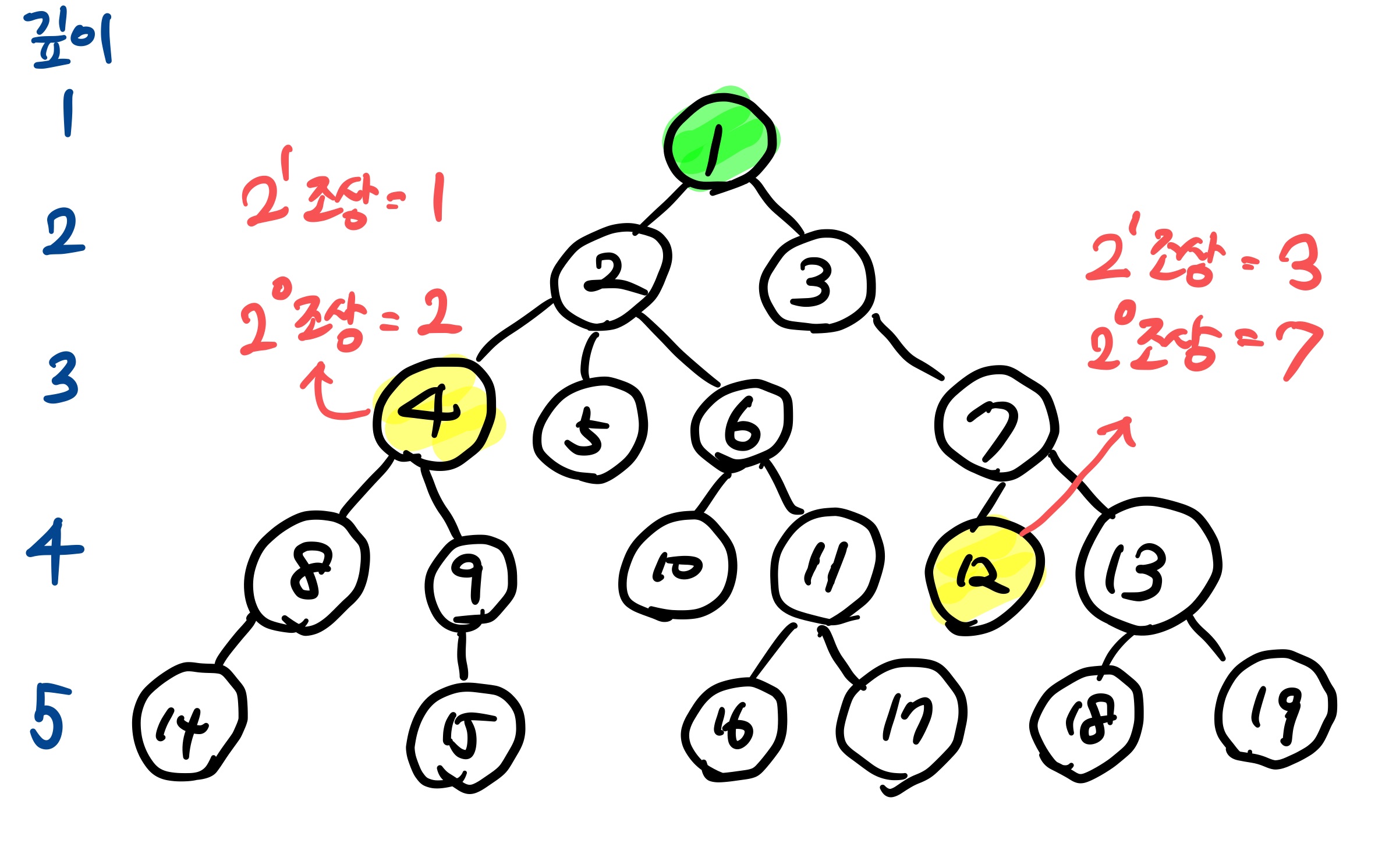
이런 식으로 4번과 12번 노드에 대해서 각각의 깊이와 2^N번째 조상을 메모했다. 그리고 나서 깊이가 더 깊은 노드를 깊이가 얕은 노드까지 올려주는 작업을 진행한다. 12번 노드가 깊이가 더 깊으므로 깊이를 4번 노드와 맞춰 준다. 이 때 2^N 번째 조상들 중 가장 큰 값부터 2^0번째 조상까지 크기 역순으로 탐색을 하면 어느 높이든지 다 도달할 수 있다. 2^1번째 조상의 경우 4번 노드보다 더 깊이가 얕으므로 안 되고, 2^0번째 조상이 4번 노드와 깊이가 같아지므로 그 지점까지 노드를 끌어 올린다.

이제 깊이가 같아졌으므로 같은 높이씩 올리면서 공통 조상을 찾아야 한다. 이 때 역시 2^N 번째 조상을 크기 역순으로 탐색하는데, 2^N 번째 조상이 같으면 패스하고, 달라질 때 마다 노드를 타고 올라간다. 이 문제에서는 4와 7의 2^2 번째 조상은 둘 다 0이므로 패스, 2^1 번째 조상도 둘 다 1이므로 패스, 2^0 번째 조상은 각각 2와 3이므로 타고 올라간다. 그 다음도 같은 과정을 반복하고 그렇게 계속 타고 올라가다 보면 LCA(4,7)이 1을 공통 조상으로 가진다는 사실을 알 수 있다.
그럼 LCA에 대해 어느정도 이해가 된 상태에서 <도로 네트워크> 문제를 풀어보자.
문제에서 N개의 노드와 N-1개의 도로가 주어졌다. 그리고 우리는 임의의 두 노드가 주어졌을 때 가장 짧은 도로와 가장 긴 도로를 찾아서 출력해야 한다. 우선 입력값으로 들어온 두 노드 사이의 도로를 담을 자료구조를 만든다. 나는 Node라는 클래스를 하나 만들어서 거리(d)와 길이(len)을 프로퍼티로 두었고, 시작 노드를 Key로 하고 그 시작 노드에 연결된 노드들의 ArrayList를 Value로 하는 HashMap 자료구조를 아래와 같이 만들어 보았다.

이렇게 만들고 나서 root 노드를 1로 설정한 뒤 DFS로 트리를 만들어 준다. 이 때 각각의 노드를 연결하면서 바로 위(2^0 번째) 부모 노드와 바로 위(2^0번째)까지의 최대, 최소 도로 길이를 dp로 저장한다.

그 이후에 각각의 노드에 대해서 2^N 번째 부모 노드와 해당 노드에서 2^N번째까지의 최단 도로 길이와 최장 도로 길이를 반복문을 돌면서 업데이트 해 준다.

예를 들어 qmin[2][1] = 50 이 의미하는 것은 노드 2에서 2^1번째 부모, 즉 여기서는 노드 1까지 최소 도로 길이가 50이라는 의미이다. 비슷하게 qmax[2][1] = 100은 노드 2에서 2^1번째 부모(노드 1)까지의 최대 도로 길이가 100이라는 의미이다.

이렇게 트리에 대해서 각각의 노드에 대한 2^N번째 부모 노드, 2^N번째 부모까지의 최단 도로, 최장 도로 값을 dp로 저장해 둔 뒤에 M개의 테스트 케이스에 대해서 서로 다른 두 노드를 입력 받으면 LCA 알고리즘을 통해 두 노드의 공통 조상 노드를 찾고 각각의 노드에서 공통 조상 노드까지 최단 도로, 최장 도로를 구한 뒤 두 최단 도로 중 더 작은 값, 두 최장 도로 중 더 큰 값을 출력하면 문제를 해결할 수 있다.

이 문제에서 내가 제출한 자바 소스코드는 다음과 같다.
조금 까다롭지만 천천히 문제를 따라가다 보면 많은 것을 배울 수 있는 문제이다. 어려워도 꼭 도전해 보기를 바란다.
'Computer Sci. > Algorithms' 카테고리의 다른 글
| 백준 2352 / LIS(최장 증가 수열), DP / JAVA (0) | 2020.06.17 |
|---|---|
| 프로그래머스 종이접기 / 이진 트리, 순회 / JAVA (0) | 2020.06.03 |
| 카카오 19겨울인턴 4번 / 유니온 파인드(Union Find) / JAVA (0) | 2020.05.11 |
| 백준 9202 / 트라이(Trie), DFS / JAVA (0) | 2020.05.08 |
| 백준 1300 / 이분 탐색 (Binary Search) / JAVA (0) | 2020.05.07 |
