SW엔지니어로서 면접을 준비하면서 기본적인 컴퓨터 사이언스 지식을 복습하는 의미에서 이렇게 블로그에 정리를 하고자 한다.
가장 먼저 복습할 과목은 자료구조이다.
이번 글에서는 배열, 그리고 해시테이블에 대해서 복습해 보려 한다.
먼저 배열부터 살펴보자.
배열
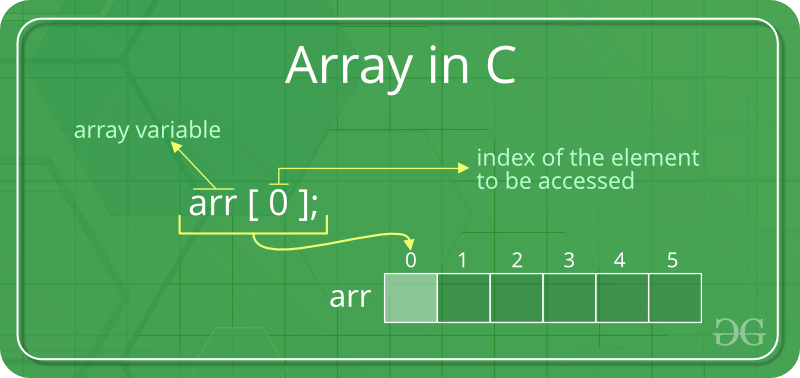
배열(array)은 연관된 데이터를 모아서 한 번에 관리하기 위해 사용하는 데이터 타입이다. 배열은 논리적인 저장순서와 물리적인 저장순서가 일치한다. 따라서 인덱스(index)를 사용하여 해당 원소에 접근할 수가 있다. 인덱스를 알고 있다면 각각의 원소를 바로 찾아갈 수 있게 되므로 원소를 찾는데 걸리는 시간복잡도는 O(1) 이라고 볼 수 있고, 이를 임의 접근(random access)이 가능하다고 말한다.
반면에 새로운 데이터를 삭제하거나 삽입을 하게 되면 조금 복잡해진다. 삭제의 경우 먼저 해당 원소에 접근을 해서 작업을 완료하는데 (O(1)), 이 상태는 배열의 연속적인 특성이 깨지게 된다. 따라서 이러한 빈 공간을 메꿔주기 위해서 삭제한 원소보다 더 큰 인덱스를 갖는 원소들을 shift 해주어야 하며, 이 때 비용이 발생하고 결과적으로 시간복잡도는 O(n)이 된다. 삽입의 경우도 비슷하게 생각해 볼 수 있다.
또한 메모리 주소가 연속되야 하기 때문에, 배열의 크기를 늘리는 것은 불가능하다. 만약 배열의 크기를 늘려야 할 필요가 있다면, 크기가 큰 배열을 만들어서 기존 내용을 복사하거나, 연결 리스트(LinkedList)를 사용하는 방법을 생각해 보아야 한다.
// A character array in C/C++/Java
char arr1[] = {'g', 'e', 'e', 'k', 's'};
// An Integer array in C/C++/Java
int arr2[] = {10, 20, 30, 40, 50};
// Item at i'th index in array is typically accessed
// as "arr[i]". For example arr1[0] gives us 'g'
// and arr2[3] gives us 40.특정 언어에서는 배열(이 경우는 종종 리스트라고 불리지만)의 크기를 자동으로 조절할 수 있다. 즉, 데이터를 덧붙일 때마다 배열 혹은 리스트의 크기가 증가한다. 하지만 자바 같은 언어는 배열의 길이가 고정되어 있다. 이런 경우에는 배열을 만들 때 배열의 크기를 함께 지정해야 한다. 그래서 동적 가변 크기 기능이 내재되어 있는 배열과 비슷한 자료구조를 원할 때는 보통 ArrayList를 사용한다. ArrayList는 필요에 따라 크기를 변화시킬 수 있으면서도 O(1)의 접근시간을 유지한다.
해시 테이블
해시테이블(HashTable)은 해시 함수를 사용하여 키를 해시값으로 매핑하고, 이 해시값을 인덱스 혹은 주소로 삼아서 데이터의 값을 키와 함께 저장하는 자료구조이다. 먼저 이해해야 할 개념은 해싱과 해시 함수(hash function)이다.

해시 함수란 데이터의 효율적 관리를 목적으로 임의의 길이 데이터를 고정된 길이 데이터로 매핑하는 함수이다. 이 때 매핑 전 원래 데이터 값을 키(key), 매핑 후 데이터 값을 해시값(hash value), 매핑하는 과정 자체를 해싱(hashing)이라고 한다. 이와 같이 해싱을 하게 되면, 적은 리소스를 가지고 많은 데이터를 효율적으로 관리할 수 있게 된다. 예를 들면 해시 함수를 통해 하드디스크나 클라우드에 존재하는 무한에 가까운 데이터(키)들을 유한한 개수의 해시값으로 매핑함으로써 작은 크기의 캐쉬 메모리로 프로세스를 관리할 수 있다.
해시 함수는 언제나 동일한 해시값을 리턴하고, 인덱스만 알면 해시 테이블이 아무리 커도 데이터에 빠르게 접근할 수 있다.(배열과 유사) 따라서 데이터에 접근하는 경우 시간복잡도는 O(1)을 지향하는 상수에 가까운 값이 나오게 된다. 배열의 경우 탐색시 시간복잡도는 O(1)이지만, 메모리를 미리 많이 할당해 두어야 하기 때문에 공간효율적이라고 보기가 어렵다.
이런 해시 테이블에도 단점이 있는데, 바로 해시 함수가 서로 다른 두 개의 키에 대해 동일한 해시값을 나타내는 충돌(collision)현상이 일어난다는 것이다. 보통 해시 테이블을 사용하면, 해시 테이블의 크기(m)가 실제 사용하는 키 개수(n)보다 적어야 하는데(메모리 리소스 문제 등), 이 때 n/m을 load factor(α)라고 부른다. load factor가 클 수록 해시 충돌 문제가 발생할 가능성이 높아진다.

충돌 문제를 해결하기 위해 나온 방법들이 여러가지가 있는데, 대표적인 두 가지 아이디어는 분리 연결법(seperate chaining)과 개방 주소법(open addressing)이다. 먼저 분리 연결법을 살펴보면 하나의 버킷당 들어갈 수 있는 엔트리의 수에 제한을 두지 않음으로서, 모든 자료를 해시테이블에 담는 것이다. 해당 버킷에 이미 데이터가 있다면 연결 리스트 방식을 사용하여 노드와 노드를 체인처럼 연결한다는 의미에서 chaining이라는 용어가 붙은 것으로 보인다. 이 방법의 장점은 유연하며, 삭제 및 삽입의 시간복잡도가 O(1)으로 빠르다는 점이 있다. 반면, 단점은 연결 리스트 자체의 제한이 없다보니 오버헤드가 부담이 되고 메모리 문제를 야기할 수 있다는 점이다.

개방 주소법은 한 버킷당 들어갈 수 있는 엔트리가 하나뿐인 해시 테이블이다. 해시함수로 얻은 주소가 아닌, 다른 주소에 데이터를 저장할 수 있도록 허용한다는 취지에서 open addressing이라는 이름이 붙은 것으로 보인다. 이 방법의 경우, 해시 충돌이 발생하면 (삽입하려는 해시 버킷이 이미 사용중인 경우) 다른 해시 버킷에 해당 자료를 삽입한다. 이 때 다른 해시 버킷을 찾는 탐사 과정을 probing이라고 한다. 분리 연결법의 장점은 캐시 효율이 높고 메모리 문제가 발생할 가능성은 적지만, 해시 충돌이 발생할 가능성이 분리 연결법에 비해서 높으며 특정 해시값이 키가 몰리게 되면 효율성이 급격하게 떨어진다는 단점이 있다.
참고자료
- https://github.com/JaeYeopHan/Interview_Question_for_Beginner/tree/master/DataStructure
- https://github.com/jwasham/coding-interview-university/blob/master/translations/README-ko.md#%EB%B0%B0%EC%97%B4
- https://www.geeksforgeeks.org/array-data-structure/
- https://ratsgo.github.io/data%20structure&algorithm/2017/10/25/hash/
- <코딩인터뷰 완전분석>, 게일 라크만 맥도웰 저
'Computer Sci. > Data Structure' 카테고리의 다른 글
| DS #5. 그래프 (Graph) (0) | 2019.10.08 |
|---|---|
| DS #4. 트리와 힙 (Tree and Heap) (0) | 2019.10.04 |
| DS #3. 스택과 큐 (Stack and Queue) (0) | 2019.09.27 |
| DS #2. 연결 리스트 (LinkedList) (0) | 2019.09.26 |
