이번 포스팅에서는 그래프 자료구조에 대해서 공부해 본다.

그래프
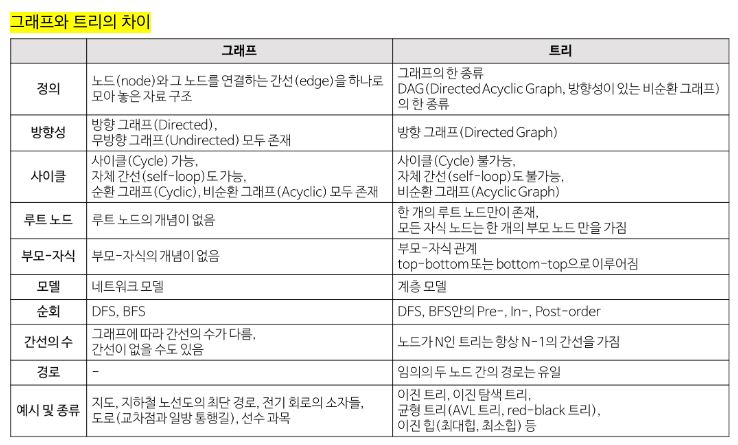
그래프(Graph)는 노드(node)와 그 노드를 연결하는 간선(edge)을 하나로 모아놓은 자료구조이다. 즉, 연결되어 있는 객체 간의 관계를 표현할 수 있다. 예를 들면 지하철에서 다른 역으로 가는 최단 경로를 찾아주는 서비스도 그래프 알고리즘을 사용한다. 그래프의 한 종류로 트리 자료구조가 있는데 그래프와 트리의 차이는 다음과 같다.
그래프 관련 용어를 정리하면 다음과 같다. 먼저 정점과 간선의 연결 관계에서 방향성을 가지는 지를 가지고 나누어 볼 수 있다. 방향성이 없는 그래프를 무향 그래프(Undirected Graph)라 하고, 방향성이 포함되어 있는 그래프를 유향 그래프(Directed Graph)라고 한다. 무향 그래프에서 각 정점(vertex)에서 연결된 Edge의 갯수를 차수(degree)라고 한다. 유향 그래프에서는 간선에 방향성이 존재하기 때문에 차수가 두 개로 나뉜다. 각 정점으로부터 나가는 간선의 갯수를 진출 차수(out-degree), 들어오는 간선의 갯수를 진입 차수(in-degree)라고 한다. 또한 경로를 구성하는 데 사용된 간선의 수는 경로 길이(path length)라고 한다. 경로 중에서 반복되는 정점이 없는 경우는 단순 경로(simple path)라고 하는데, 이 때 단순 경로의 시작 정점과 종료 정점이 동일한 경우를 사이클(cycle)이라고 부른다.
그래프를 나누는 기준에 따라서 여러가지 종류가 있는데, 앞서 살펴본 것처럼 방향이 있는지 없는지에 따라서도 유향 그래프, 무향 그래프로 나눌 수 있다. 또한 간선에 비용이나 가중치가 있으면 가중치 그래프(Weighted Graph)라고 하며, 다른 말로는 '네트워크' 라고도 한다. 무방향 그래프에서 모든 정점쌍에 대해 항상 경로가 존재하면 연결 그래프(Connected Graph), 적어도 하나의 정점쌍에서 경로가 존재하지 않는다면 비연결 그래프(Disconnected Graph)라고 부른다. 만약에 그래프에 속해 있는 모든 정점이 서로 연결되어 있다면, 그 그래프는 완전 그래프(Complete Graph)라고 부른다.


그래프를 구현하는 방법에는 인접 리스트(Adjacency List)를 사용하는 방법과 인접 행렬(Adjacency matrix)을 사용하는 방법 크게 두 가지가 있다. 먼저 인접 리스트를 살펴보면 그래프를 표현함에 있어 각각의 정점에 인접한 정점들을 연결 리스트로 표시한 것이다. 각 연결 리스트의 노드들은 인접 정점을 저장하게 된다. 정점의 수가 n개이고 간선의 수가 e개인 무방향 그래프를 표시하기 위해서는 n개의 연결 리스트가 필요하고, n개의 헤드 포인터와 2e개의 노드가 필요하다. 따라서 인접 리스트 표현은 간선의 갯수가 적은 희소 그래프(sparse graph)의 표현에 적합하다. 그리고 이 때 전체 간선의 수를 알아내려면 헤더 노드를 포함하여 모든 인접 리스트를 조사해야 하므로 O(n+e)의 연산이 요구된다. 아래는 위의 그림에 해당하는 무방향 그래프를 C++과 JAVA로 구현한 코드이다.
C++
// A simple representation of graph using STL
#include<bits/stdc++.h>
using namespace std;
// A utility function to add an edge in an
// undirected graph.
void addEdge(vector<int> adj[], int u, int v)
{
adj[u].push_back(v);
adj[v].push_back(u);
}
// A utility function to print the adjacency list
// representation of graph
void printGraph(vector<int> adj[], int V)
{
for (int v = 0; v < V; ++v)
{
cout << "\n Adjacency list of vertex "
<< v << "\n head ";
for (auto x : adj[v])
cout << "-> " << x;
printf("\n");
}
}
// Driver code
int main()
{
int V = 5;
vector<int> adj[V];
addEdge(adj, 0, 1);
addEdge(adj, 0, 4);
addEdge(adj, 1, 2);
addEdge(adj, 1, 3);
addEdge(adj, 1, 4);
addEdge(adj, 2, 3);
addEdge(adj, 3, 4);
printGraph(adj, V);
return 0;
} JAVA
// Java Program to demonstrate adjacency list
// representation of graphs
import java.util.LinkedList;
public class GFG
{
// A user define class to represent a graph.
// A graph is an array of adjacency lists.
// Size of array will be V (number of vertices
// in graph)
static class Graph
{
int V;
LinkedList<Integer> adjListArray[];
// constructor
Graph(int V)
{
this.V = V;
// define the size of array as
// number of vertices
adjListArray = new LinkedList[V];
// Create a new list for each vertex
// such that adjacent nodes can be stored
for(int i = 0; i < V ; i++){
adjListArray[i] = new LinkedList<>();
}
}
}
// Adds an edge to an undirected graph
static void addEdge(Graph graph, int src, int dest)
{
// Add an edge from src to dest.
graph.adjListArray[src].add(dest);
// Since graph is undirected, add an edge from dest
// to src also
graph.adjListArray[dest].add(src);
}
// A utility function to print the adjacency list
// representation of graph
static void printGraph(Graph graph)
{
for(int v = 0; v < graph.V; v++)
{
System.out.println("Adjacency list of vertex "+ v);
System.out.print("head");
for(Integer pCrawl: graph.adjListArray[v]){
System.out.print(" -> "+pCrawl);
}
System.out.println("\n");
}
}
// Driver program to test above functions
public static void main(String args[])
{
// create the graph given in above figure
int V = 5;
Graph graph = new Graph(V);
addEdge(graph, 0, 1);
addEdge(graph, 0, 4);
addEdge(graph, 1, 2);
addEdge(graph, 1, 3);
addEdge(graph, 1, 4);
addEdge(graph, 2, 3);
addEdge(graph, 3, 4);
// print the adjacency list representation of
// the above graph
printGraph(graph);
}
}
// This code is contributed by Sumit Ghosh
인접 행렬은 NXN boolean 행렬로써 matrix[i][j] = true 라면 i -> j 로의 간선이 있다는 뜻이다. 정점의 갯수가 N인 그래프를 인접 행렬로 표현하면 간선의 수와 무관하게 항상 N^2의 메모리 공간이 필요하다. 또한 무방향 그래프를 인접 행렬로 표현한다면 이 행렬은 대칭 행렬(Symmetric Matrix)이 된다. 인접 행렬의 경우 간선이 많이 존재하는 밀집 그래프(dense graph)를 표현하는 데에는 적합하나 희소 그래프(sparse graph)에는 메모리의 낭비가 크므로 적합하지 않다. 인접 행렬을 이용하면 두 정점을 연결하는 간선의 존재 여부를 O(1)으로 즉시 알 수 있다는 장점이 있다. 그러나 그래프에 존재하는 모든 간선의 수를 알아내려면 인접행렬 전체를 조사해야 하므로 N^2번의 조사가 필요하게 되어 O(N^2)의 시간이 요구된다.
그래프의 탐색에는 크게 두 가지의 방법이 있다.
-
깊이 우선 탐색(DFS, Depth First Search)
- 루트 노드(혹은 다른 임의의 노드)에서 시작해서 다음 분기(branch)로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법
- 즉, 넓게(wide) 탐색하기 전에 깊게(Deep) 탐색하는 것이다.
- 모든 노드를 방문하고자 하는 경우 이 방법을 선택한다.
- 깊이 우선 탐색은 그래프의 모든 간선을 조사하므로 정점의 수가 n이고 간선의 수가 e인 그래프가 인접 리스트로 표현되어 있다면 O(n+e)이고, 인접 행렬로 표시되어 있다면 O(n^2)이다.
- 순환 호출 또는 스택을 사용한다.
-
너비 우선 탐색(BFS, Breadth First Search)
- 루트 노드(혹은 다른 임의의 노드)에서 시작해서 인접한 노드를 먼저 탐색하는 방법
- 즉, 깊게(deep) 탐색하기 전에 넓게(wide) 탐색하는 것이다.
- 두 노드 사이의 최단 경로 혹은 임의의 경로를 찾고 싶을 때 이 방법을 선택한다.
- 너비 우선 탐색은 그래프가 인접 리스트로 표현되어 있으면 전체 수행 시간이 O(n+e)이며, 인접 행렬로 표현되어 있는 경우는 O(n^2)의 시간이 걸린다.
- 방문한 정점들을 차례로 저장한 후 꺼낼 수 있는 자료구조인 큐를 사용한다.
참고 자료
'Computer Sci. > Data Structure' 카테고리의 다른 글
| DS #4. 트리와 힙 (Tree and Heap) (0) | 2019.10.04 |
|---|---|
| DS #3. 스택과 큐 (Stack and Queue) (0) | 2019.09.27 |
| DS #2. 연결 리스트 (LinkedList) (0) | 2019.09.26 |
| DS #1. 배열과 해시테이블 (Array and HashTable) (0) | 2019.09.25 |
