
이번 포스팅에서는 킥스타트 2020 Round F에 대한 문제 풀이를 공유하고자 한다.
1. ATM Queue

나는 이 문제를 우선순위 큐를 가지고 풀었다. 배열에 담겨진 각각의 출금액을 A1, A2, A3, ... , An 이라고 했을 때 그 출금액의 인덱스(몇 번째에 출금을 하는지)와 1회 최대 출금액(X)으로 나눈 몫을 가지고 클래스를 만들어서 출금액 몫 오름차순, 그리고 몫이 같을 경우 인덱스 오름차순이 되게 클래스의 기준을 만들어서 우선순위 큐에 넣으면 자동으로 정렬이 되어서 출력된다. 시간복잡도는 O(NlogN)
2. Metal Hervest

이 문제는 그리디 알고리즘으로 풀었다. 추수 기간이 오버랩 되지 않는다고 해서(These time intervals do not overlap) 문제가 수월하게 풀렸던 것 같다 ㅎㅎ 추수 시작과 끝을 저장할 수 있는 클래스를 만들어서 각각의 추수 기간을 객체로 만들어서 리스트에 저장한다. 그리고 정렬을 하는데 추수가 끝나는 시간을 기준으로 오름차순 정렬을 하면 시간 순서대로 정렬이 된다.
첫 로봇을 작동하는 시간은 이 리스트의 첫번째 추수가 시작하는 시간으로 잡는다. 그 시간을 T 라고 하고 로봇이 한 번 동작하는 시간을 K 라고 하면 이 로봇이 추수를 끝내는 시점은 T+K 가 될 것이다. 그러면 그 때 해당 추수가 끝나는지 아닌지를 판단하는데, 만약 이 때 추수가 덜 끝났으면 바로 다시 새로운 로봇을 추수하도록 동작시켜야 한다. 이 때 추수가 끝났다면 그 다음 추수가 시작하는 시점에 새로운 로봇을 추수하도록 동작시킨다.

이렇게 되면 시간복잡도 O(NlogN)으로 문제를 해결할 수 있다.
3. Painter's Duel
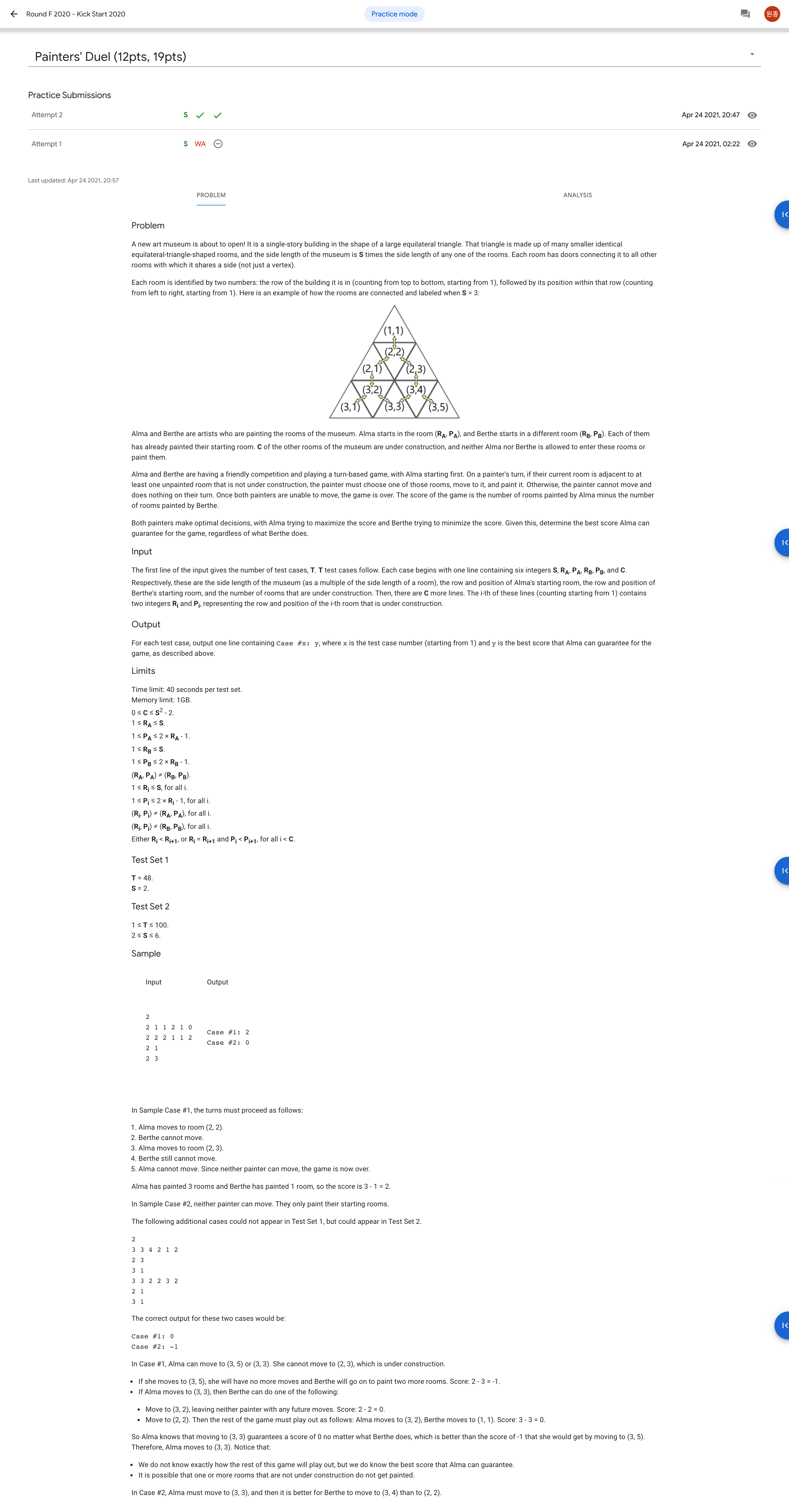
이 문제는 게임 이론 중 하나인 minmax 알고리즘을 가지고 풀었다. minmax 알고리즘이란 틱택토나 체스처럼 두 명이 대결을 할 때 한 사람은 최상의 결과를 내려 하고 한 사람은 최하의 결과를 내려 하는데 이를 번갈아 가면서 점수를 계산할 때 사용하는 알고리즘이다. Minimax Algorithm in Game Theory
이 문제에서 Alma는 점수를 최대로 만들려고 하고, Berthe는 점수를 최소로 만들려고 한다. 그리고 문제에서 구하라는 것은 Alma가 받을 수 있는 최대의 점수가 아니라, Berthe가 어떤 결정을 하더라도 Alma가 보장할 수 있는 최대의 점수이다. 따라서 여기서 가장 중요하게 알아야 할 점은 Alma의 차례에서는 최대 점수를 낼 수 있는 방법을 찾아야 하고, Berthe의 차례에서는 최소 점수를 낼 수 있는 방법을 찾아야 하며 이를 번갈아 가면서 진행해야 한다는 점이다.
문제에서 주어진 예제를 하나 보도록 하자 처음에 A는 (3, 4)에서, B는 (2, 1)에서 시작하며, 공사중이라 갈 수 없는 방이 (2, 3), (3, 1) 이렇게 두 개가 있다.

먼저 A는 양 옆인 (3, 3) 또는 (3, 5) 중에 한 군데를 갈 수가 있다.

그리고 B 역시 마찬가지로 인접한 (2, 2)나 (3, 2) 중 한 군데를 갈 수 있을 것이다.

여기까지를 놓고 보면 다음과 같이 트리 형태로 가능한 경우의 수를 생각해 볼 수 있다. 번갈아 가면서 Max, Min 으로 스코어를 가져가려는 점을 기억하자.

처음에 A는 무조건 점수를 높게 가져가려 할 것이다. 왼쪽을 선택하면 가능한 점수가 0만 있고, 오른쪽을 선택하면 가능한 점수가 -1만 있으므로 A는 왼쪽으로 (3, 5)를 선택할 것이다. 그 이후에 B는 어느쪽을 선택하는 점수가 0이므로 어느 쪽이나 선택할 수 있고 결과적으로 이 게임에서 보장할 수 있는 최소한의 점수의 최대값은 0임을 알 수 있다.
이 문제에서 S 즉 삼각형의 한 변의 크기가 최대 6이라고 했으므로 예상할 수 있는 시간복잡도는 O(2^(S^2))이다 하지만 중간중간 걸러지는 케이스가 많아서 시간 초과가 일어나지는 않는다.
'Computer Sci. > Algorithms' 카테고리의 다른 글
| [알고리즘 문제 해결 전략] Ch02. 알고리즘 분석 (1) | 2022.03.04 |
|---|---|
| 백준 14500 / 테트로미노 / Brute Force / JAVA / 골드 5 (0) | 2021.10.09 |
| [킥스타트] Google Kick Start 2020 Round E 문제 풀이 (0) | 2021.03.29 |
| [킥스타트] Google Kick Start 2020 Round D 문제 풀이 (0) | 2021.01.06 |
| [킥스타트] Google Kick Start 2020 Round C 문제 풀이 (0) | 2020.12.22 |
