
이번 포스팅에서는 킥스타트 2020 Round E에 대한 문제 풀이를 공유하고자 한다.
이전 문제풀이
1. Longest Arithmatic
주어진 배열을 한 번 반복문을 돌면서 가장 긴 등차수열을 찾으면 쉽게 풀 수 있는 문제이다. 시간복잡도는 O(N)
2. High Buildings
이 문제는 전체 빌딩 숫자, 왼쪽에서 Andre가 바라본 건물의 숫자, 오른쪽에서 Sule가 바라본 건물의 숫자, 그리고 두 명이 같이 볼 수 있는 건물의 숫자를 입력받아 각각의 건물들이 가질 수 있는 높이의 예시를 출력하면 되는 문제이다. 만약 가능한 경우가 없으면 "IMPOSSIBLE"을 출력한다. 조금 케이스 분류를 해 주는 부분이 복잡한데 이것만 잘 해주면 정답을 쉽게 구할 수 있다.
먼저 Andre와 Sule이 같이 볼 수 있는 건물이 C개가 있는데 이들을 먼저 배치한다. 건물의 높이가 같은 경우도 볼 수 있다고 하였으므로 C개의 건물은 모두 최대 높이인 N으로 배치해도 문제가 될 것은 없다. 건물 높이는 LinkedList를 사용해서 값을 넣어주었다.
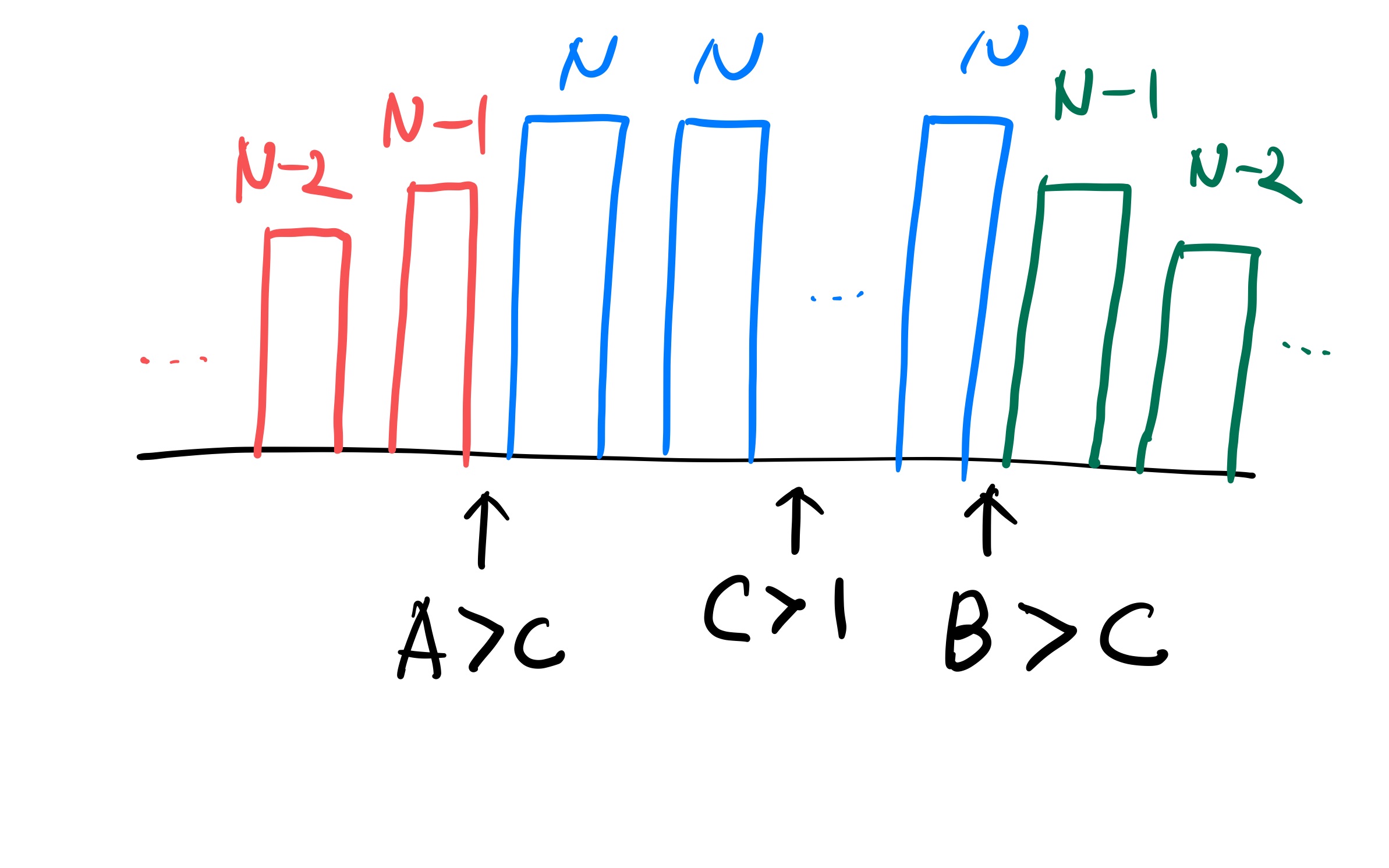
그리고 나서 Andre의 관점에서 보면 총 A개의 건물을 볼 수 있는데 이미 C개의 건물이 N개로 지어졌으므로 (A-C)개의 건물을 더 지어주어야 한다. 이 건물들이 모두 다 보이기 위해 건물은 ... (N-3) (N-2) (N-1) N N N ... 이렇게 배치가 되게 할 수 있다. 뒤에 N의 높이는 앞서 지었던 C개의 건물을 의미하고 그 앞에 하나씩 높이를 낮춰가면서 (A-C)개의 건물을 짓는다.
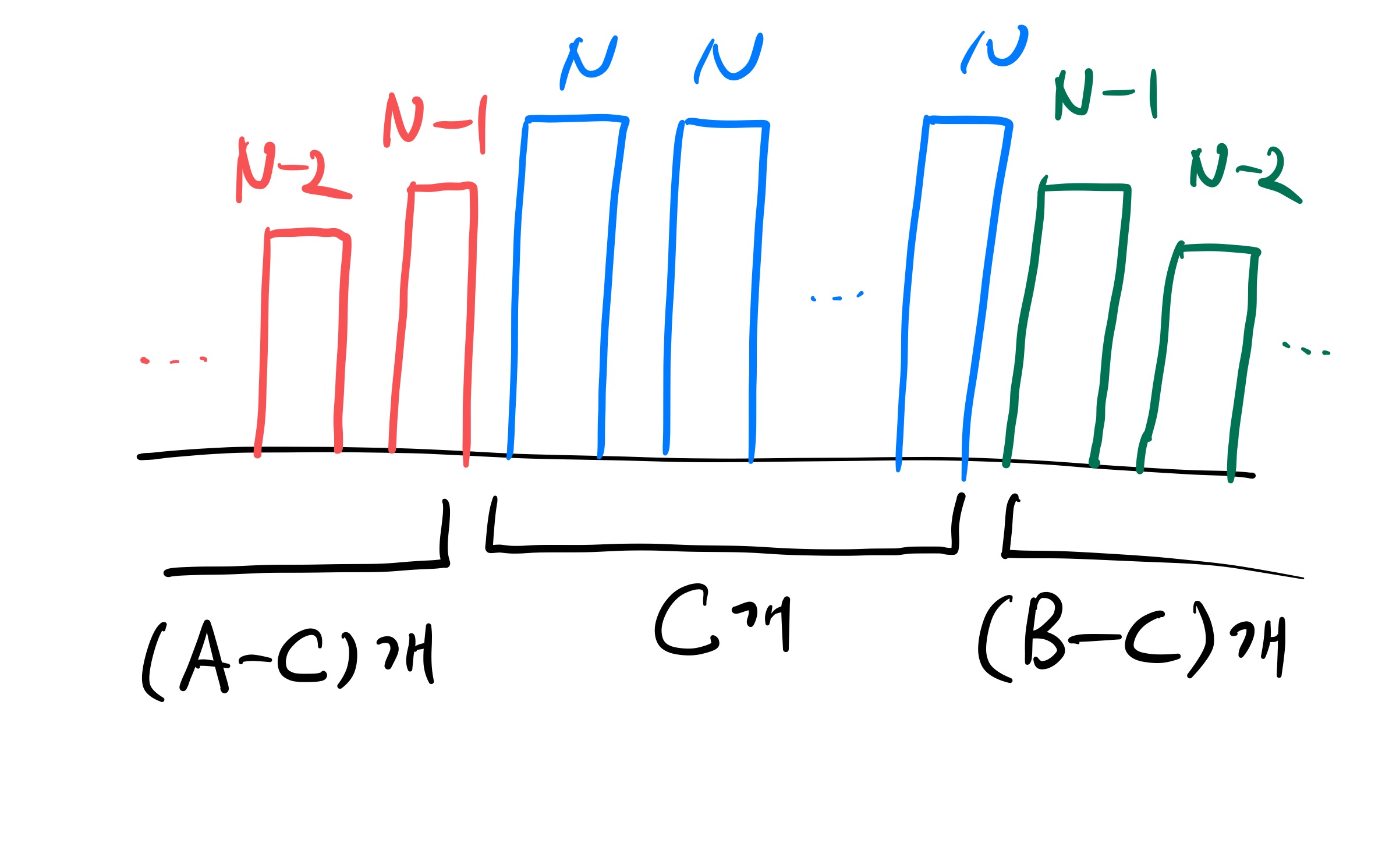
비슷한 방법으로 Sule이 볼 수 있는 건물도 짓는다. (B-C)개의 건물을 더 지어주어야 하며 Sule에 눈에 다 보이게 지으려면 ... N N N (N-1) (N-2) (N-3) ... 이렇게 지을 수 있다. 그러면 지금까지 지은 건물의 갯수는 (A-C) + C + (B-C) = A+B-C 개의 건물을 지었다. 그러므로 지금 이 LinkedList의 size는 A+B-C 이다.
그리고 나서 나머지 건물은 Andre와 Sule의 눈에 보이지 않게 지어야 한다. 지을 수 있는 건물의 가장 낮은 높이는 1이고, 지어야 할 건물의 갯수는 N-(A+B-C) 개이다. 그리고 이 때 높이가 1인 건물을 어디에 지어야 할지는 C가 2개 이상인지 아니면 A > C 인지, B > C인지 등등 케이스를 나누어서 위치를 잡아주어야 하고 불가능한 경우는 "IMPOSSIBLE"을 출력하면 된다.
이렇게 솔루션을 만들었을 때 시간복잡도는 O(N)이다.
3. Toys
이 문제는 각각의 장난감들이 E(Enjoy), R(Remember) 값을 가지고 있으며 원형으로 배열을 해서 지루함 없이 무한하게 놀 수 있는지, 아니면 유한하게 놀 수 있는지를 알아보는 문제이다. 먼저 N개의 장난감에 대해서 E, R 값을 ArrayList 로 저장한다. 그리고 전체 사이클이 지속되는 시간, 즉 지금 가지고 노는 장난감부터 다음 번 이 장난감 차례가 오기 전까지의 즐거움을 느끼는 시간을 CurrentCycle로 잡는다. (currentCycle = E1+E2+...+En)
그 이후에 우선순위 큐(Priority Queue)를 가지고 각각의 장난감이 쿨타임(Rk+Ek) 값으로 정렬이 되는 큐를 만든다. 이 값은 k번째 장난감을 가지고 놀고(Ek) 그 이후 기억하는 시간(Rk)을 더한 값으로 쿨타임에 해당이 되며, 1번 장난감부터 순서대로 하나씩 빼도 문제가 없는지를 체크하기 위함이다. 그렇게 값과 인덱스가 포함된 클래스 Element를 만들어서 반복문을 돌려주면서 우선순위 큐에 값을 하나씩 넣는다. 가장 긴 쿨타임이 currentCycle보다 더 작거나 같다면 이 경우는 무한하게 돌 수 있으므로 장난감을 우선순위 큐에서 빼지 않고 넘어간다.
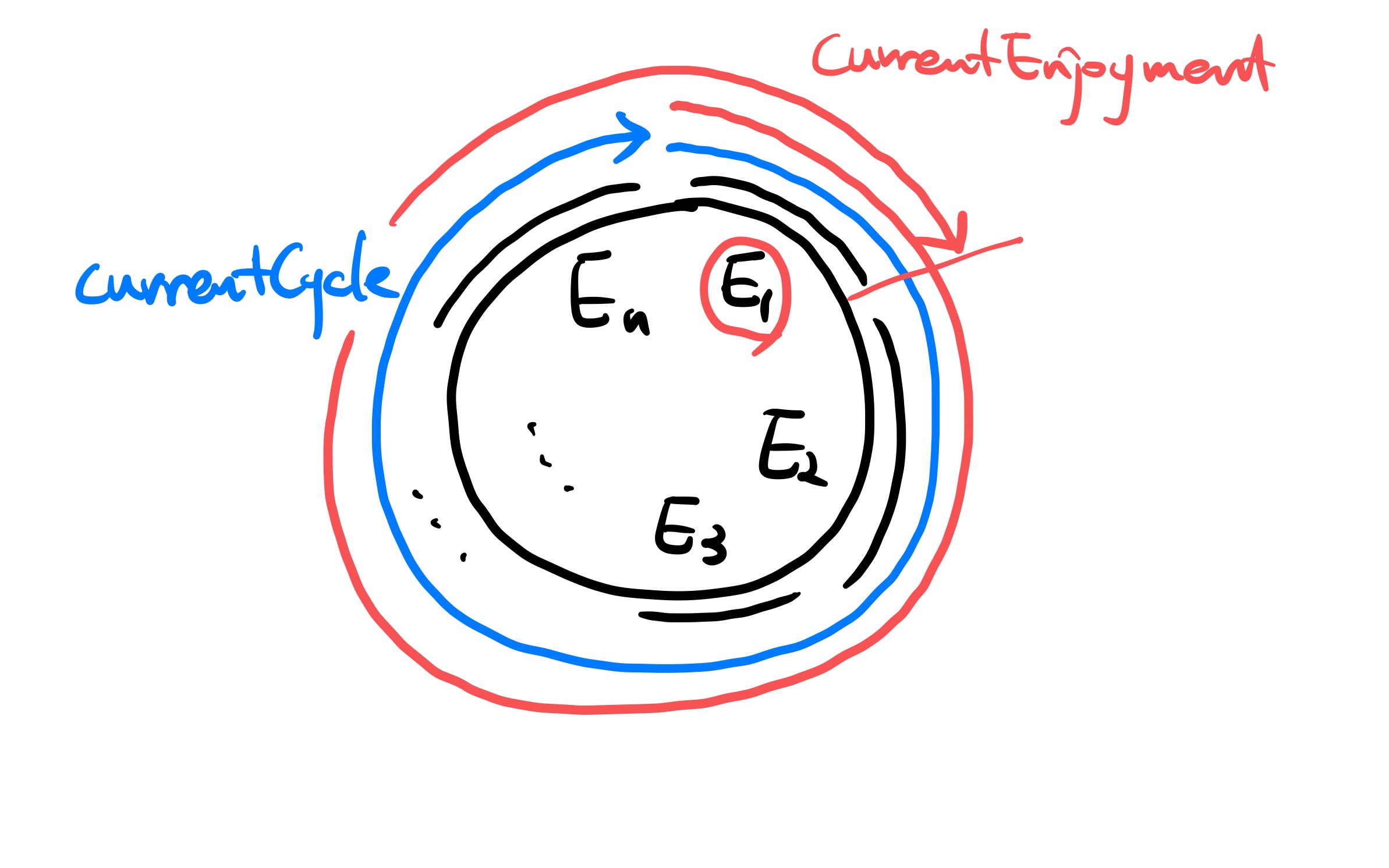
반면 최대 쿨타임이 currentCycle 보다 크면 무한하게 놀지 못하고 싫증을 낸다. 따라서 이 때는 가장 쿨타임이 긴 값을 빼서 무한하게 놀 수 있는 조합을 찾아야 한다. k번째 장난감을 빼면서 currentCycle에 Ek 값을 빼준다. 이 때 currentEnjoyment는 현재 k번째 장난감을 가지고 놀 때 가질 수 있는 즐거움의 시간이다. 이 값은 currentCycle + Ek 값으로 이루어 진다. 따라서 k번째 장난감을 빼 줄 때는 현재 값에서 2*Ek 값을 빼주고 그 다음 장난감에서 다시 E값을 더해주어서 진행한다.
'Computer Sci. > Algorithms' 카테고리의 다른 글
| 백준 14500 / 테트로미노 / Brute Force / JAVA / 골드 5 (0) | 2021.10.09 |
|---|---|
| [킥스타트] Google Kick Start 2020 Round F 문제 풀이 (0) | 2021.04.28 |
| [킥스타트] Google Kick Start 2020 Round D 문제 풀이 (0) | 2021.01.06 |
| [킥스타트] Google Kick Start 2020 Round C 문제 풀이 (0) | 2020.12.22 |
| [킥스타트] Google Kick Start 2020 Round B 문제 풀이 (1) | 2020.12.03 |
