
이번 포스팅에서는 킥스타트 2020 Round C에 대한 문제 풀이를 공유하고자 한다.
1. Countdown
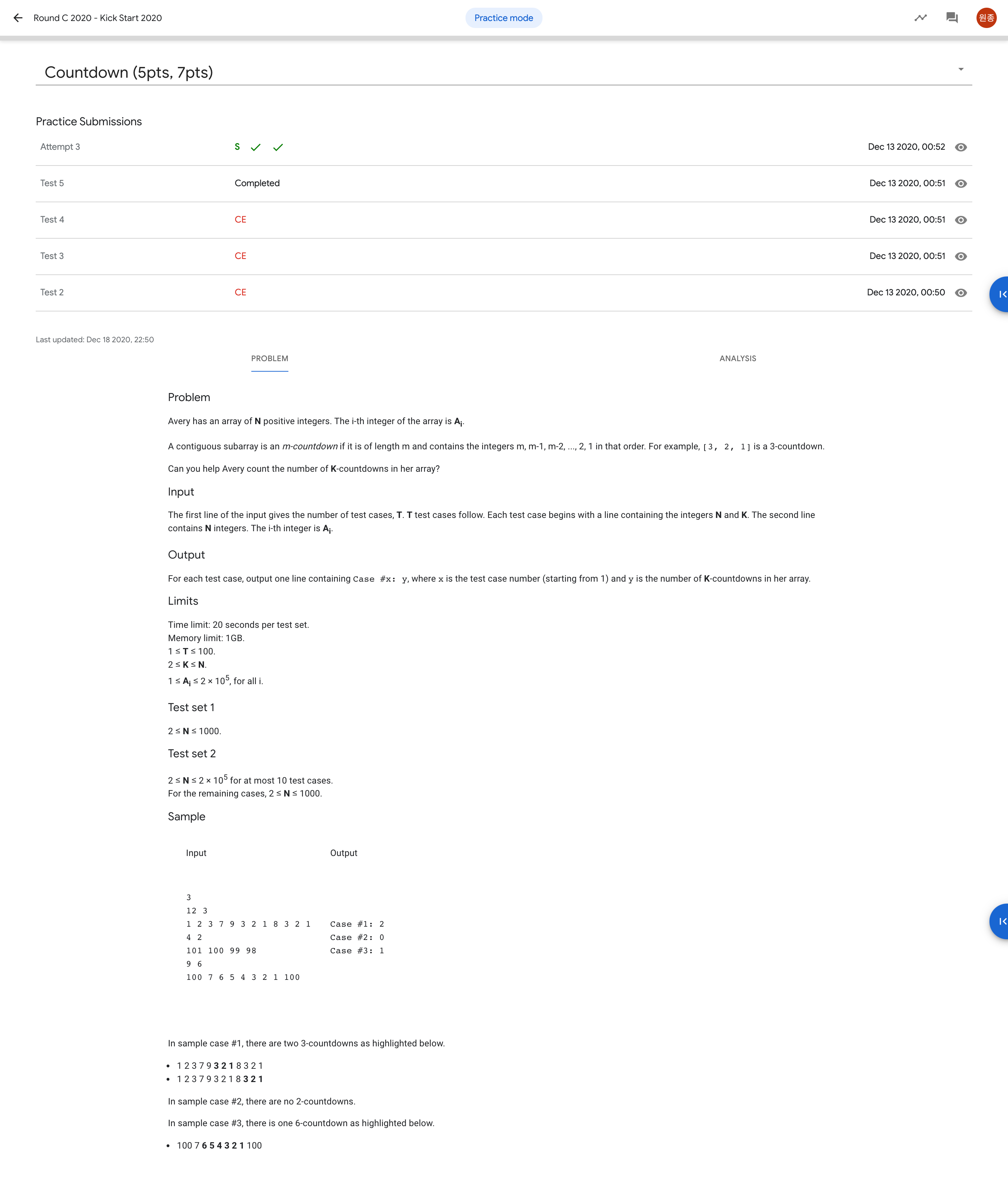
간단한 배열 문제이다. 배열의 반복문을 돌면서 주어진 숫자부터 시작되는 카운트 다운이 총 몇 개인지를 세어 주면 된다. 한 번 배열을 순환해서 답을 구할 수 있기 때문에 시간복잡도는 O(N).
2. Stable Wall
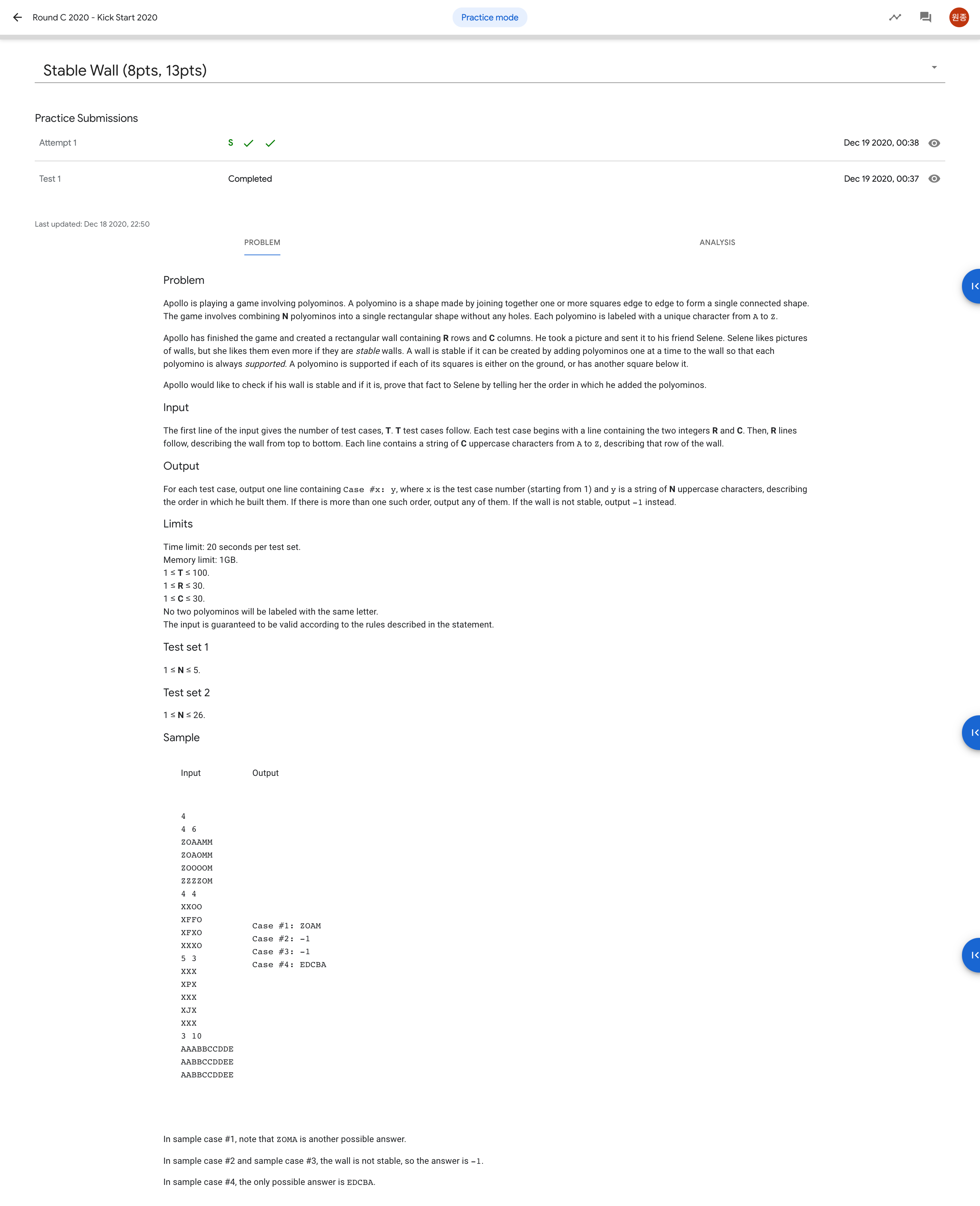
그래프 개념을 가지고 풀어야 하는 조금 까다로운 문제이다. 나의 경우 다른 사람의 풀이를 조금 참고하면서 풀었다. 문제를 이해하는 것 부터 쉽지가 않았던 것 같다. 위상 정렬(topological sort)과 DFS를 사용하였다.
N개의 폴리노미노(polynomino)가 있고 이것들이 stable한 경우, 즉 각각의 폴리노미노가 바닥에 붙어 있거나, 다른 폴리노미노 위에 올라타 있을 때 폴리노미노를 쌓는 순서를 출력하면 된다. 만약 stable 하지 않는 경우는 -1을 출력한다.
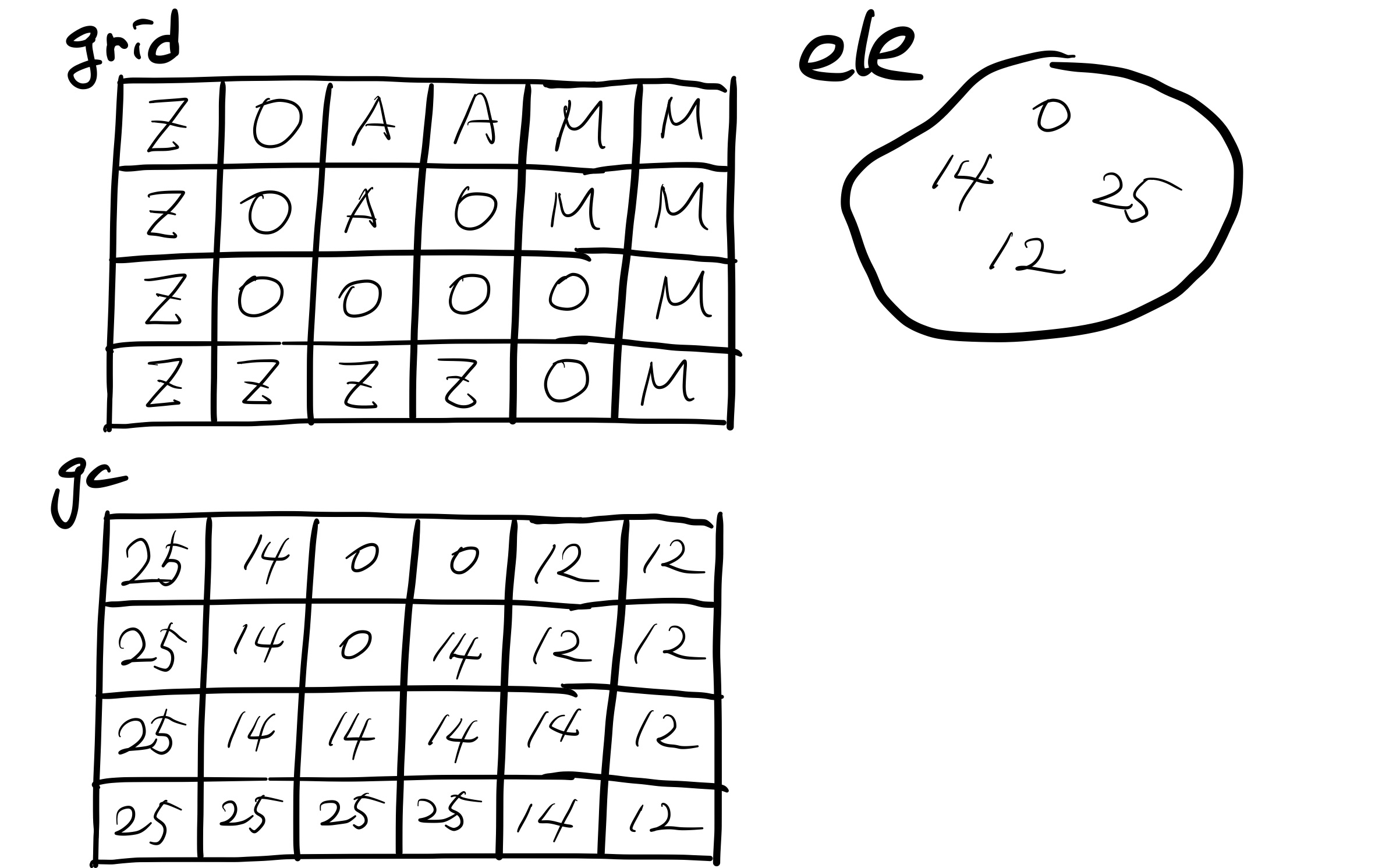
먼저 input값을 grid 2차원 배열에 받는다. 그리고 A: 0, B: 1, ... , Z: 25로 계산하여 해당 값을 담은 2차원 배열을 또 하나 만든다. 그리고 나서 해당 2차원 배열에서 한 번이라도 나왔던 값들이 포함된 집합 ele을 만든다.
그리고 나서 알파벳 순서대로 하나씩 탐색을 하면서 각각의 행(column)에서 아래부터 어떠한 알파벳 순으로 쌓아야 하는지를 찾는다. 예를 들어 3번째 행을 보면 가장 아래에 Z가 있고 그 위에 O, 그리고 나서 A가 있음을 알 수 있다. 이 말은 Z를 쌓고 그 다음 A를 쌓고, 그 다음 O를 쌓을 수 있다는 것이다. 이렇게 각각의 폴리노미노를 쌓는 순서를 graph라는 집합배열(HashSet Array)에 넣는다. graph[0]에는 A를 쌓고 나서 쌓을 수 있는 알파벳을 넣는 식으로 말이다.

그리고 나면 그래프가 완성이 된다. 이 그래프는 방향성이 있으면서 순환 구조는 없는 그래프여야 한다. 이와 같이 위상정렬이 가능한 그래프를 DAG(Directed Acyclic Graph)라고 한다. 그리고 나면 이 그래프를 알파벳 역순으로 DFS 탐색을 한다. 위의 예제에서는 알파벳 Z에서 시작하며 Z(25) -> O(14) -> M(12) -> A(0) 순으로 탐색이 이루어질 것이다. 만약 이 과정에서 순환이 발견되면 false를 반환하고 -1를 출력할 수 있는 flag도 하나 만들어 놓는다.
이 문제의 시간복잡도는 기본적으로 O(R * C + N)이 걸린다. 따라서 주어진 시간 제한 내에 풀 수 있다.
3. Perfect Subarray

이 문제도 참 쉬워보였지만 그렇게 보기보다 호락호락하지 않은 문제였던 것으로 기억한다. 어떤 배열이 주어지고 그 배열의 부분 배열 중 모든 원소의 합이 정수의 제곱수인 것들의 갯수를 구하는 문제이다. 그냥 브루트 포스로 풀면 1번은 어찌 맞겠지만.. 2번은 맞힐 수가 없다.
이 문제를 풀기 위해 나는 prefixSum 의 값을 사용하기로 했다. 그리고 여기서는 Map 자료구조를 사용했다. 키 값은 sum값, 즉 0번째 부터 i번째까지의 원소의 합을 말한다. value값은 그 sum 값이 나타난 횟수를 넣는다. 문제를 보면 원소의 값이 -100에서 100사이의 값이라고 하였으므로 동일한 sum 값이 두 번 이상 충분히 나올 수가 있다. 예를 들면 배열이 [2,4,6,-10] 이렇게 되었을 때 sum 값은 0(default), 2, 6, 12, 2 이렇게 나와서 Map 구조로 하면 { 0: 1, 2: 2, 6: 1: 12: 1 } 이렇게 나타낼 수가 있다.
그렇게 prefixSum 값을 해당 배열을 한 번 반복하면서 하나씩 업데이트를 한다. 먼저 Key = 0, Value = 1인 경우를 기본값으로 하나 넣고 시작한다. 그러면서 이 때 부분 배열의 합이 정수의 제곱이 되는 경우를 확인하는 방법은 다음과 같다.

여기서 조금 수학적인 생각이 필요한데 prefixSum - (prefixSumMap의 어떤 키값) = 정수의 제곱 이 성립되면 이 경우는 문제의 조건을 만족한다. 따라서 이 식을 조금 바꾸어 보면 prefixSum - (정수의 제곱) = prefixSumMap의 어떤 키값을 만족해야 한다. 여기서 prefixSum은 해당 arr 배열을 첫 번째부터 N번째까지 돌면서 탐색하고 (정수의 제곱)에서 정수는 0부터 하나씩 늘려가면서 역시 반복문으로 탐색한다. 그러면서 이 조건을 만족하는 prefixSumMap의 어떤 키값이 있을 경우 그 Key 값에 대한 Value 값을 정답에 더해주면 되는 것이다.
첫 번째 원소까지 돌 때는
- 30-0^2 = 30,
- 30-1^2 = 29,
- 30-2^2 = 26,
- 30-3^2 = 21,
- 30-4^2 = 14,
- 30-5^2 = 5
정수값을 하나씩 올려가는 것은 prefixSum - (정수의 제곱) >= prefixSumMap의 최소 키값인 조건에서만 반복한다. 이를 보면 첫 번째 원소를 돌 때는 조건을 만족하는 키값이 없다.
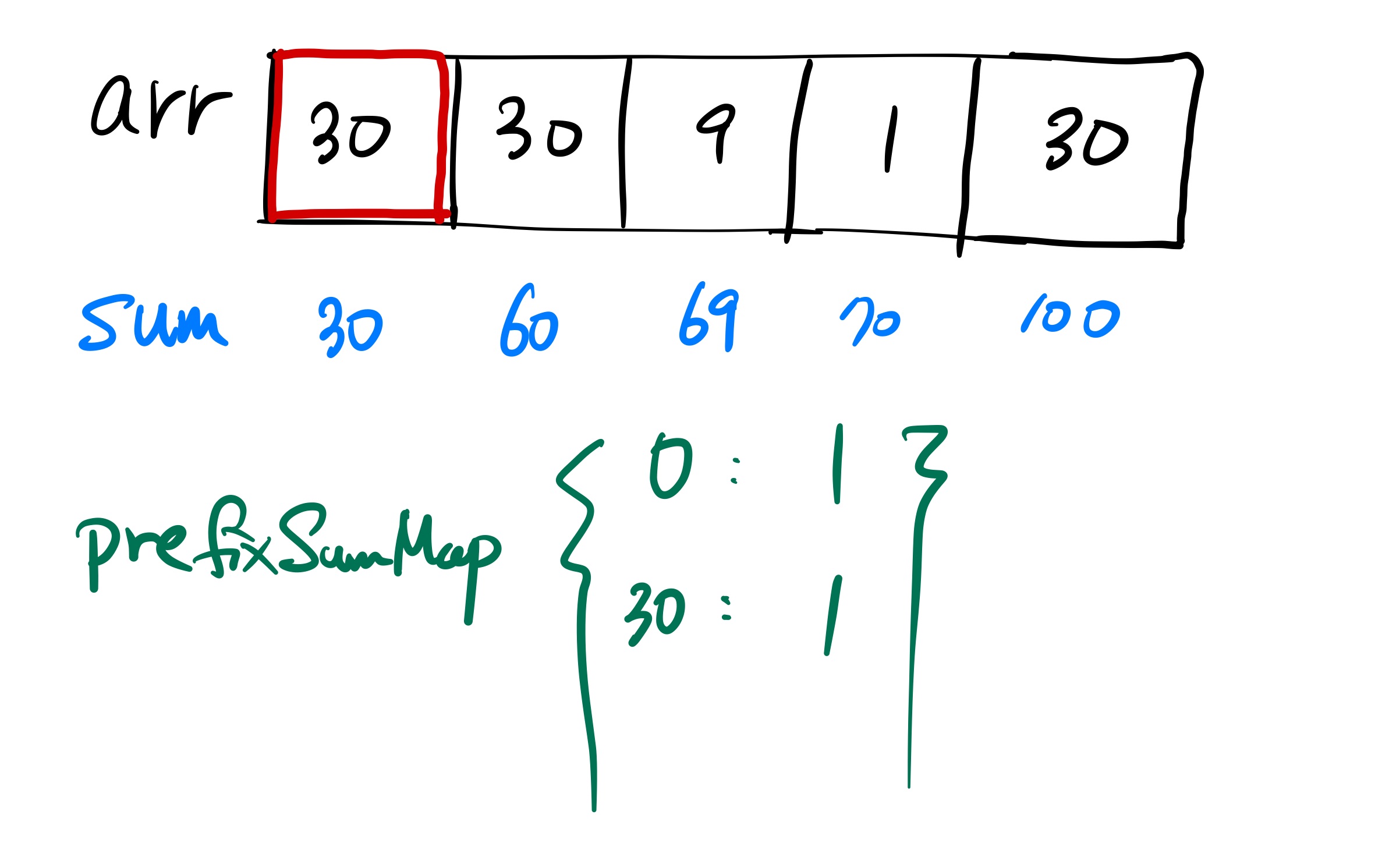
두 번째 원소에 대해서도 없다.
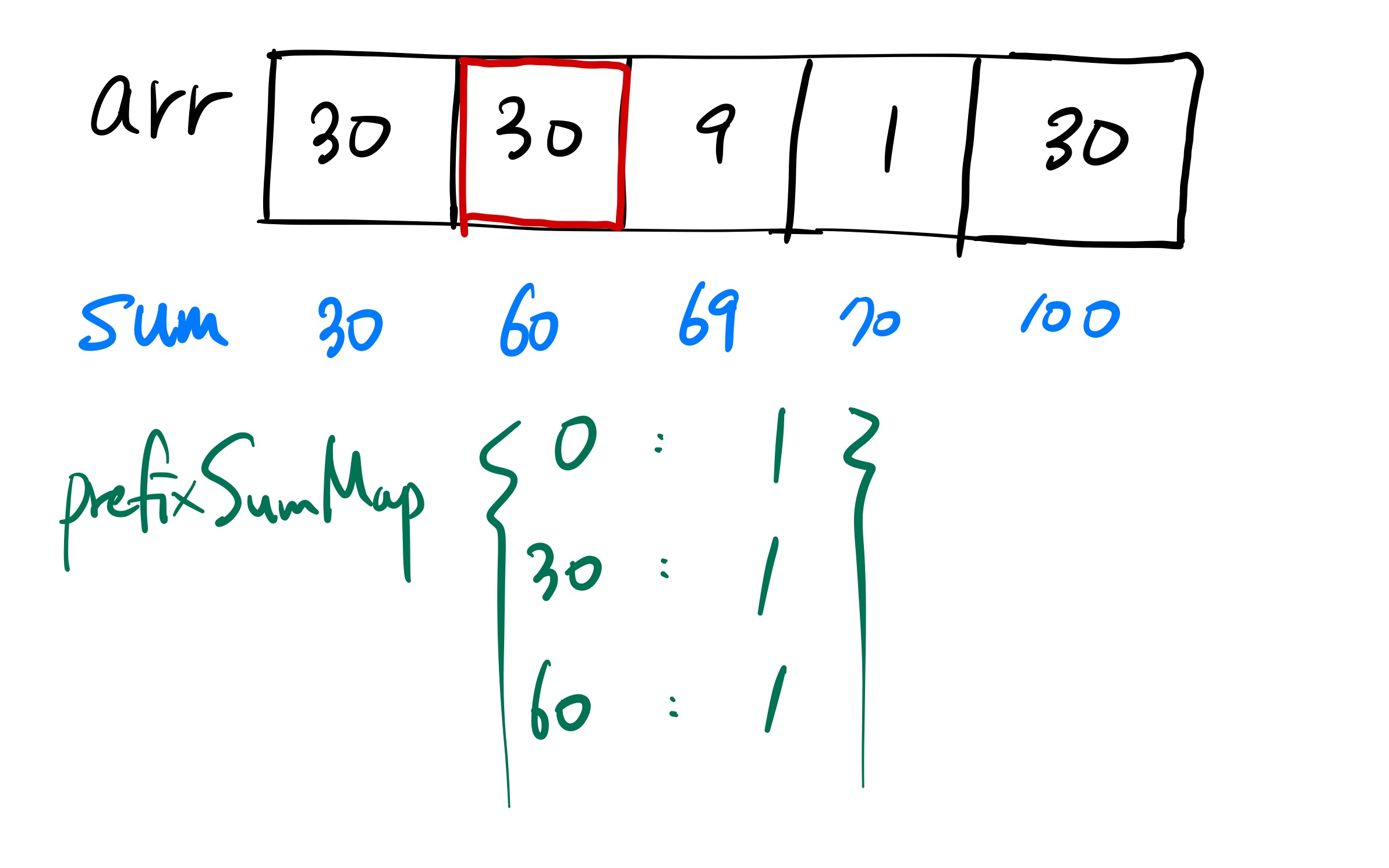
세 번째 원소의 경우는 찾을 수가 있다. prefixSum이 현재 69이고 여기에서 3의 제곱인 9를 빼면 60인데 이 키값은 맵에 있고, 이 키값에 대한 밸류값이 1이므로(즉, 지금까지 한 번만 나왔다는 의미) 구해야 하는 답(cnt)에 1을 더해준다.
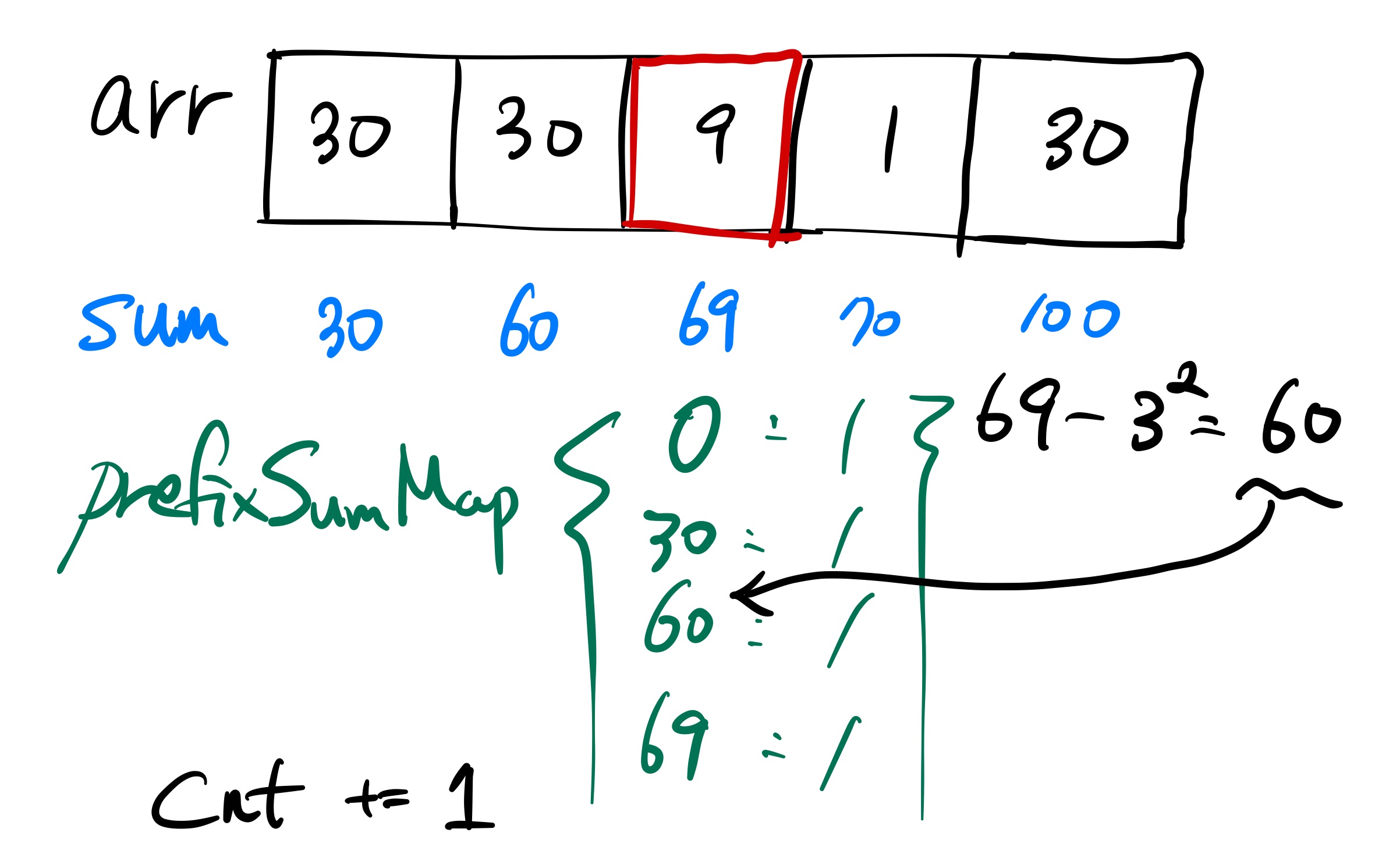
이렇게 arr 배열의 끝까지 반복한다.

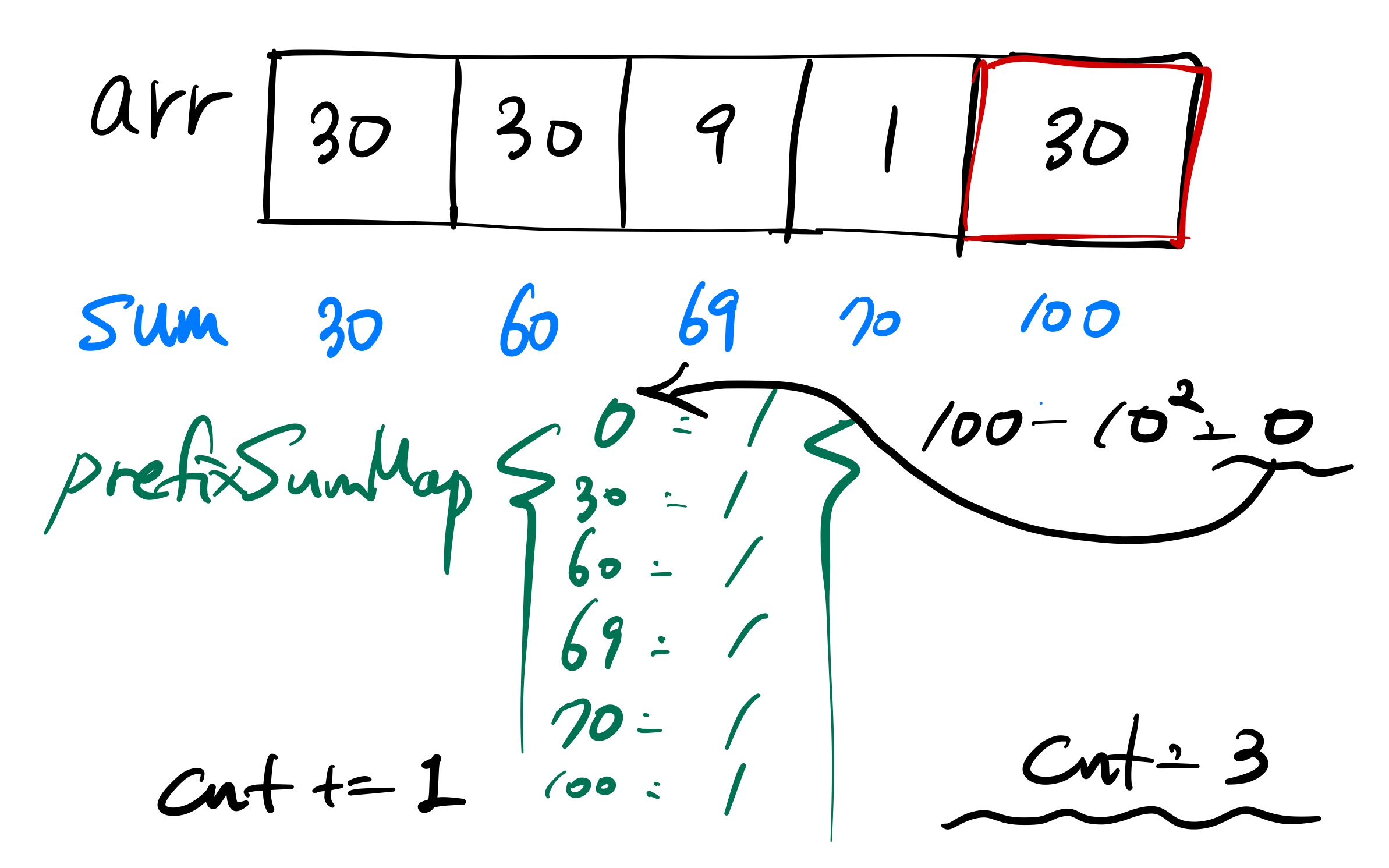
이 문제에 대한 시간복잡도는 O(N*√(N*MAX_A)) 으로 볼 수 있다. N이 문제에서 100,000이고 MAX_A=100이므로 문제에서 주어진 시간 제한 안에 통과를 할 수 있는 풀이이다.
4. Candies
항상 그랬듯이... 4번은 못 풀었다.. 여기까지 건드리긴 아직 실력이 많이 부족한 듯 하다 ㅠㅠㅠ
'Computer Sci. > Algorithms' 카테고리의 다른 글
| [킥스타트] Google Kick Start 2020 Round E 문제 풀이 (0) | 2021.03.29 |
|---|---|
| [킥스타트] Google Kick Start 2020 Round D 문제 풀이 (0) | 2021.01.06 |
| [킥스타트] Google Kick Start 2020 Round B 문제 풀이 (1) | 2020.12.03 |
| [킥스타트] Google Kick Start 2020 Round A 문제 풀이 (0) | 2020.10.07 |
| 백준 3012 / 올바른 괄호 문자열 / DP, 분할 탐색 / JAVA / 플레티넘 3 (0) | 2020.09.15 |
