
지금까지 백준만 풀다가 올해 남은 기간동안에는 구글 킥스타트 문제들을 좀 풀어보기로 했다. 구글 킥스타트는 구글에서 매년 개최하는 알고리즘 대회이다. 전 세계의 수만명이 참가하여 코딩 실력을 겨룬다. 1년에 여러 차례 대회가 열리는데(2020년 기준 한 달에 한 번꼴) 매번 대회가 끝나면 등수가 공개되어서, 객관적인 나의 수준도 판단할 수 있다. 매년 조금씩 바뀌지만 올해는 각 라운드당 3시간동안 네 문제를 푸는 형식으로 진행이 되고 있다.
나는 올해 중반부터 시작했고, 처음이다보니 아직 문제를 막 잘 풀지는 못했다. 그래서 2020년에 출제된 기출문제를 하나씩 풀어보면서 연습하고 그 내용을 블로그에 정리해 보려고 한다.
총 4문제 중에 4번 문제는 못 풀었고, 1~3번 문제만 풀어서 이에 대한 간단한 설명 및 소스코드를 첨부한다.
1번 Allocation
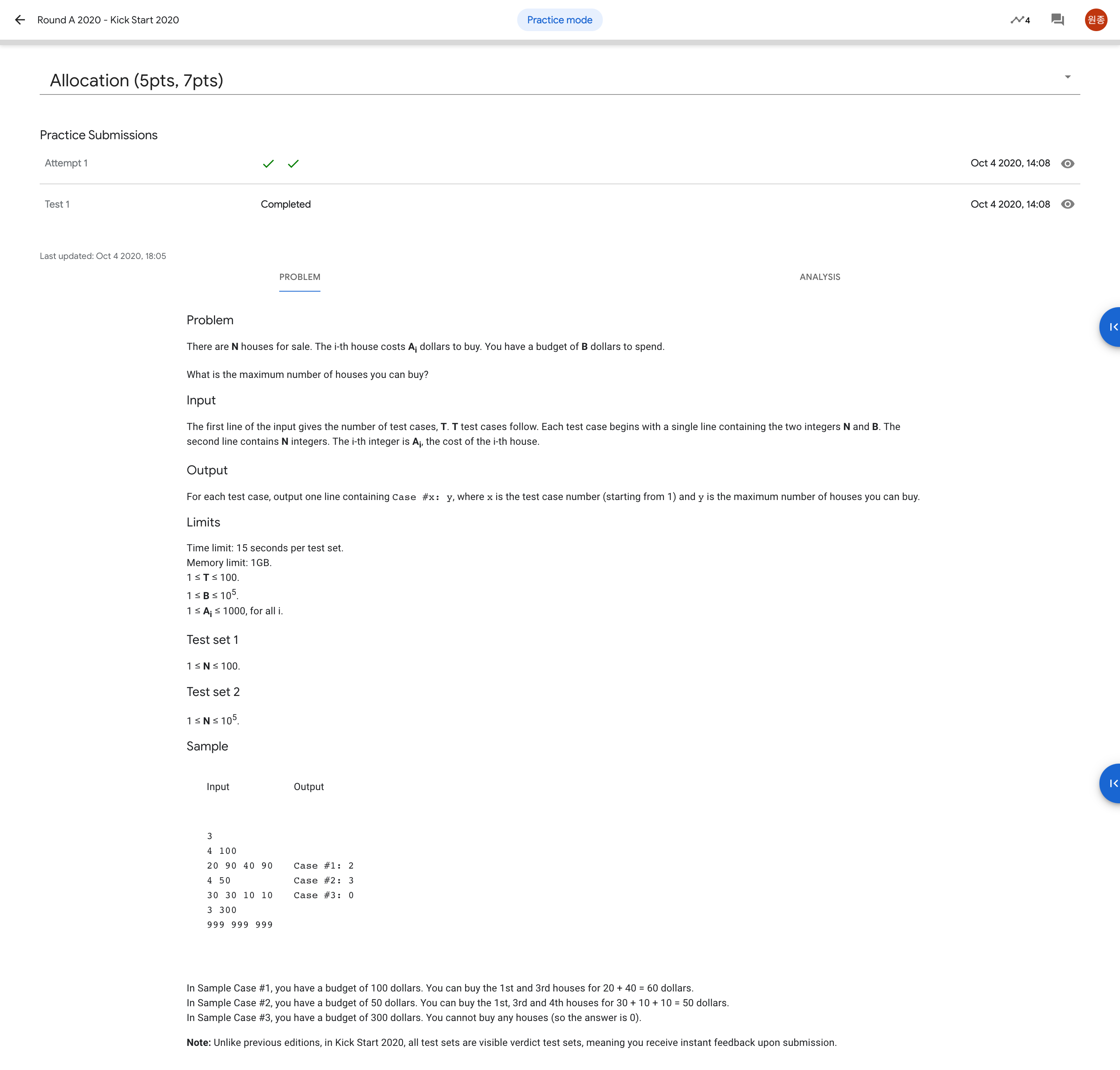
1번 문제는 크게 어렵지 않은 그리디 알고리즘 문제이다. N개의 집이 있고 B만큼의 돈이 있을 때 가장 집을 많이 산다면 몇 개까지 살 수 있는지를 묻는 문제이다. 나는 정말 단순하게 집의 가격을 오름차순으로 정렬해서 가장 싼 집부터 하나씩 구매해서 예산 B를 넘지 않는 범위까지 구매하고 그 갯수를 세어서 출력해 주었다. 이렇게 풀 경우 N개의 숫자가 있는 배열을 sort 해 주어야 하므로 O(NlogN)의 시간복잡도가 발생한다. N = 100,000이므로 시간 내에 연산이 가능하다.
2번 Plates
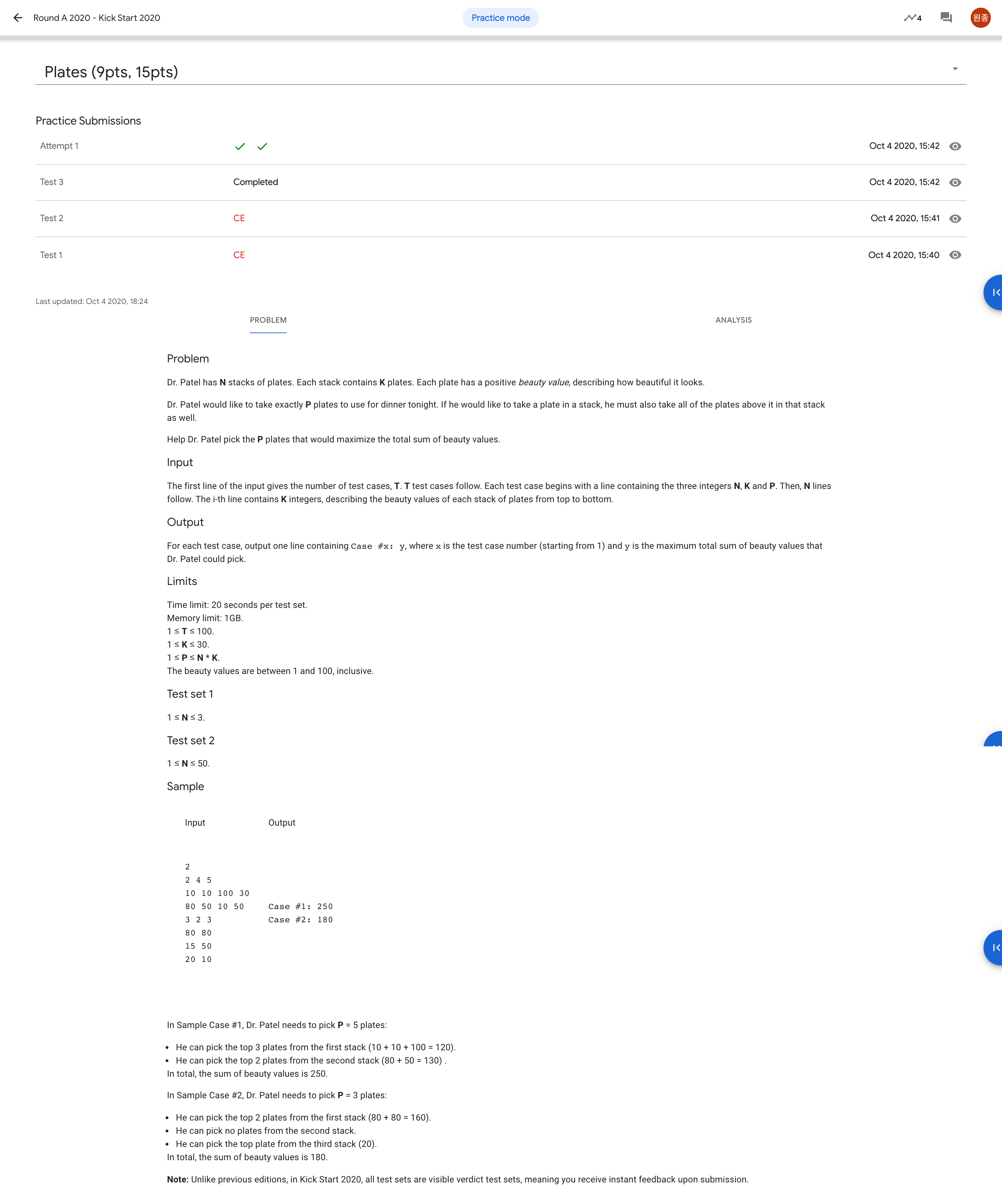
2번 문제는 DP로 풀 수 있는 문제이다. N개의 스택이 쌓여있고 각각의 스택에는 K개의 접시가 있다. 따라서 총 N*K개의 접시가 있는 것이다. 이 중에서 P개의 접시를 선택해서 가장 value가 높게 만들어야 한다. 단 조건은 어떤 스택에서 접시를 꺼낼 때 위에서부터 순서대로 꺼낼 수가 있다는 것이다.
이 문제를 풀기 위해서 나는 두 개의 배열을 사용했다. 먼저 stacks 배열이다. 이 배열은 input값을 받아서 2차원 int 형 배열로 만들어 주었다. stacks[n][k]는 n번째 스택에서 k번째 접시까지 꺼냈을 때 가치이다. 해당 스택에서 첫 번째 접시부터 k번째 접시까지 가치를 모두 더해준다. 이유는 앞서 언급한 것 처럼 k번째 접시를 꺼내기 위해서는 반드시 첫 번째 접시부터 하나씩 꺼내 주어야 하기 때문이다.
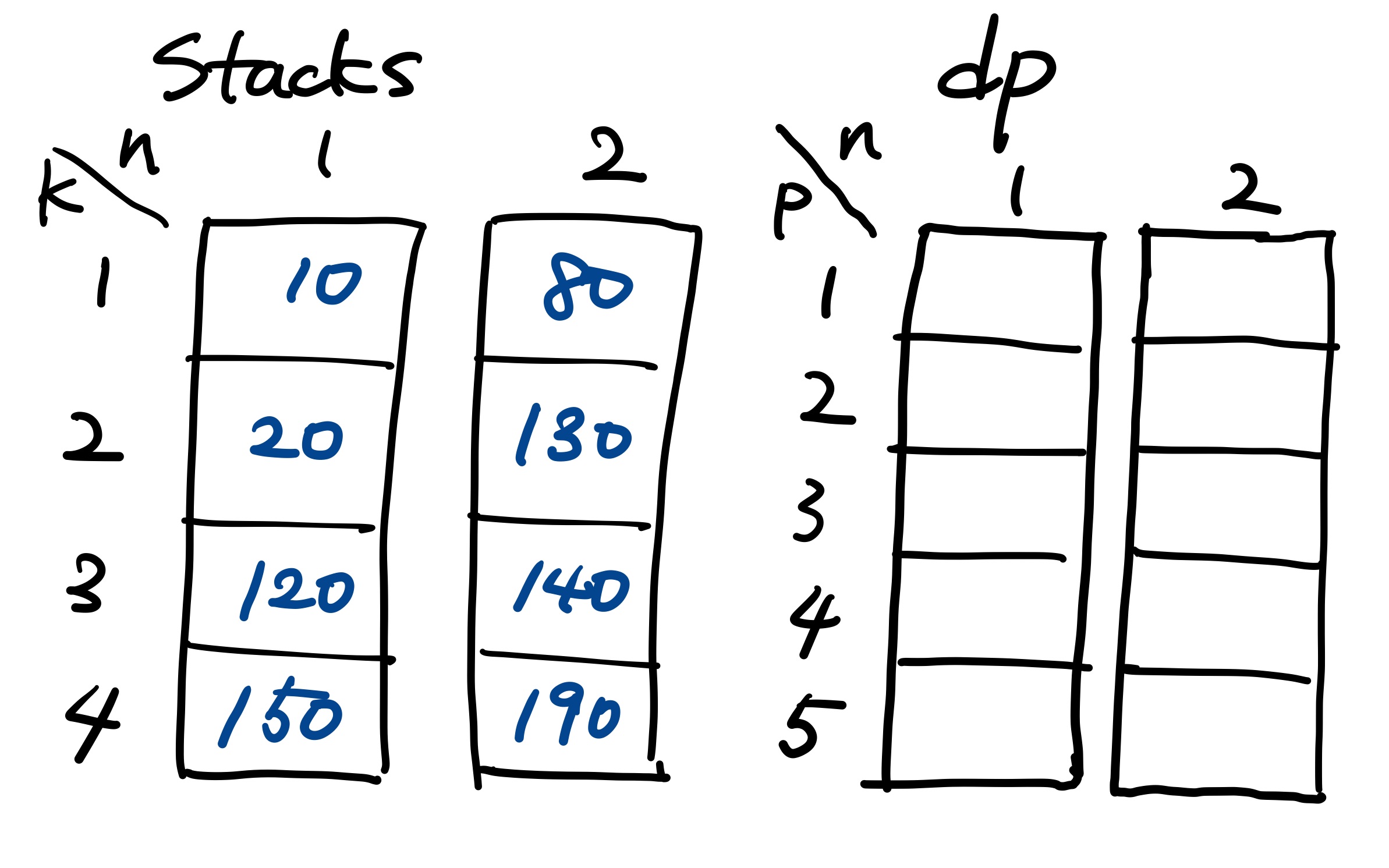
그리고 두 번째 배열은 dp 배열이다. 역시 마찬가지로 int형 2차원 배열이다. dp[n][p]는 1번째 스택부터 n번째 스택까지 p개의 접시를 골랐을 때 최대 가치를 담는다. 그리고 루프를 총 3번 돌면서(1 ... N, 1 ... P, 0 ... min(j,K)) dp 배열을 채워 나간다.
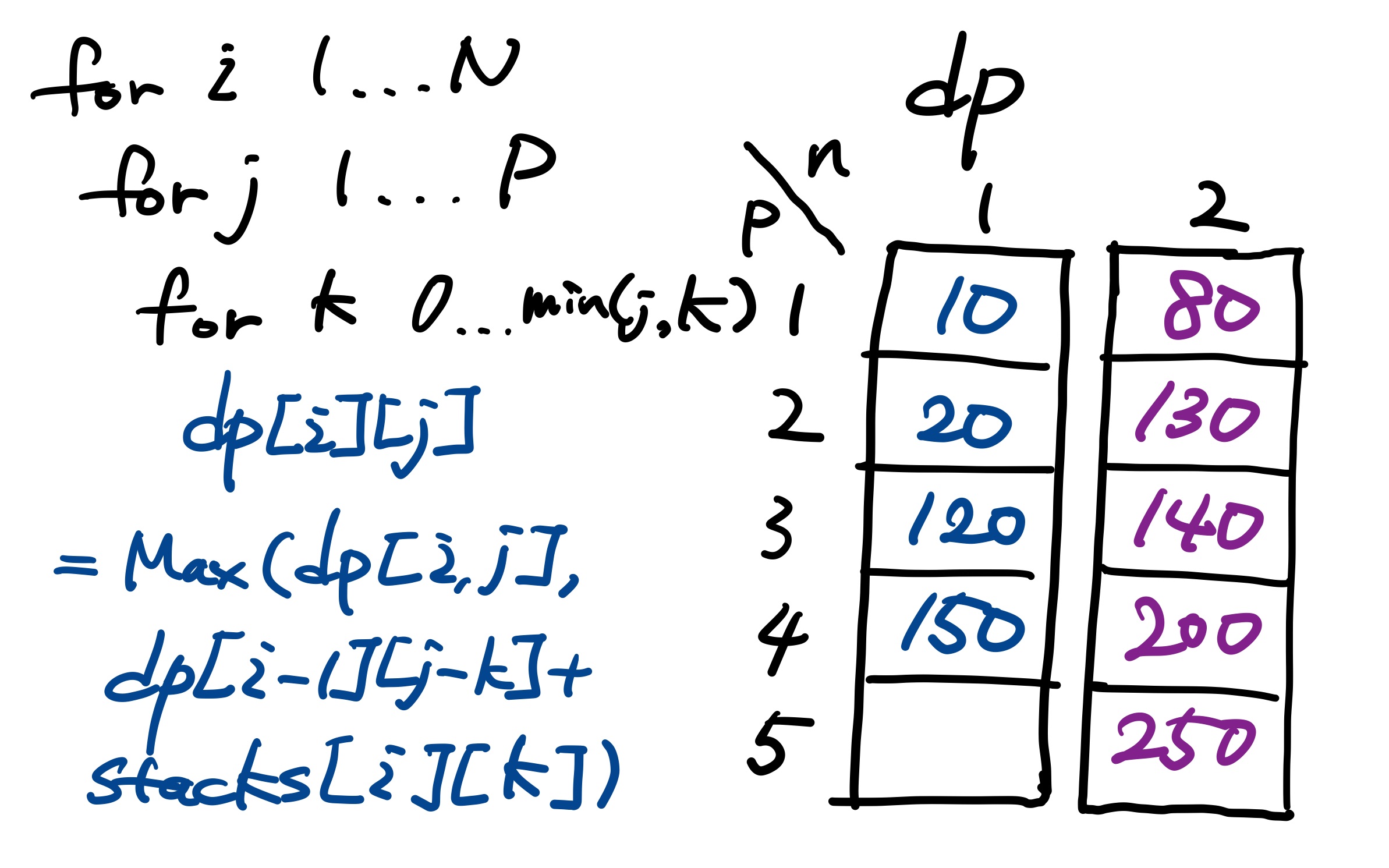
이렇게 계산을 하게 되면 dp[N][P]가 N개의 스택에서 총 P개의 접시를 조건에 맞게 꺼냈을 때 가질 수 있는 최대 가치가 나오게 된다. 시간복잡도는 O(N*P*K)로 충분히 시간 안에 계산이 가능하다.
3번 Workout
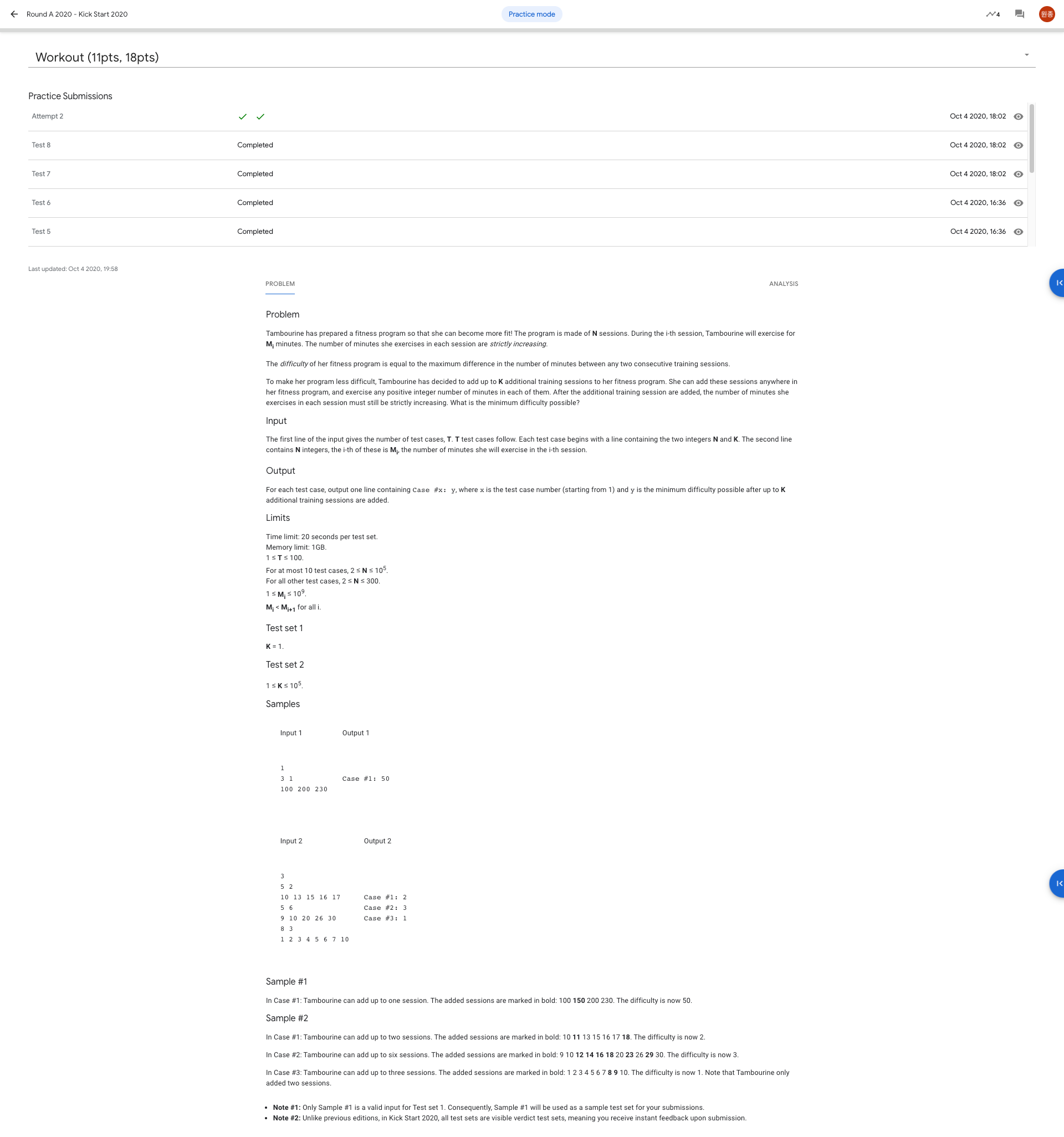
3번 문제는 살짝 까다롭다. N개의 세션이 주어지고 각각이 실행되는 시간이 증가수열로 주어진다. 인접한 두 세션 사이의 시간 간격이 난이도가 되는데 난이도를 최대한 낮춰야 한다. 난이도는 주어진 모든 세션에 대해서 발생되는 난이도의 최대값이다. 그래서 K개의 세션을 더 넣어서 만들 수 있는 최소 난이도를 구하는 것이 문제이다.
나는 처음에 우선순위 큐로 접근을 했었다. 예를 들어, 1번 예제의 경우 난이도 배열이 [100, 30] 이고 세션을 하나 추가할 수 있으므로 가장 큰 난이도를 반으로 쪼개어 [50,50,30]을 만들어서 최소 난이도가 50이라고 구하는 것처럼 말이다. 우선순위 큐로 난이도 배열의 원소들을 넣어준 뒤 K값이 줄어들 때 마다 가장 높은 난이도를 하나씩 꺼내어 반띵(?) 해주면 될거라고 생각했다. 하지만 이 방식은 결과적으로 틀렸다. 예를 들어 [100, 30]에서 K=2일 경우 내가 생각한 대로라면 [25,25,50,30] 이 되어 난이도가 50이 될텐데, 만약 100 난이도를 3등분해주면 [33,33,34,30] 으로 난이도가 34가 될 수도 있기 때문이다.
그래서 나는 이분탐색(Binary Search)을 사용하기로 했다. 문제에서 가능한 세션의 시간 값이 최소 1, 최대 10^9 이라고 하였으므로 이분 탐색으로 최대 log(10^9) = 약 30번 이면 우리가 구하는 값을 찾을 수가 있다. 그렇게 mid 값을 추정하고 그 값으로 최대 난이도가 이루어질 수 있게 세션을 추가하면서 cnt를 센다. 이 때 센 cnt가 K보다 크다면 더 큰 값의 난이도를 가질 수 있다는 의미이고, cnt가 K보다 작거나 같으면 해당 mid 값보다 작은 값으로 난이도가 결정되어야 함을 의미한다.
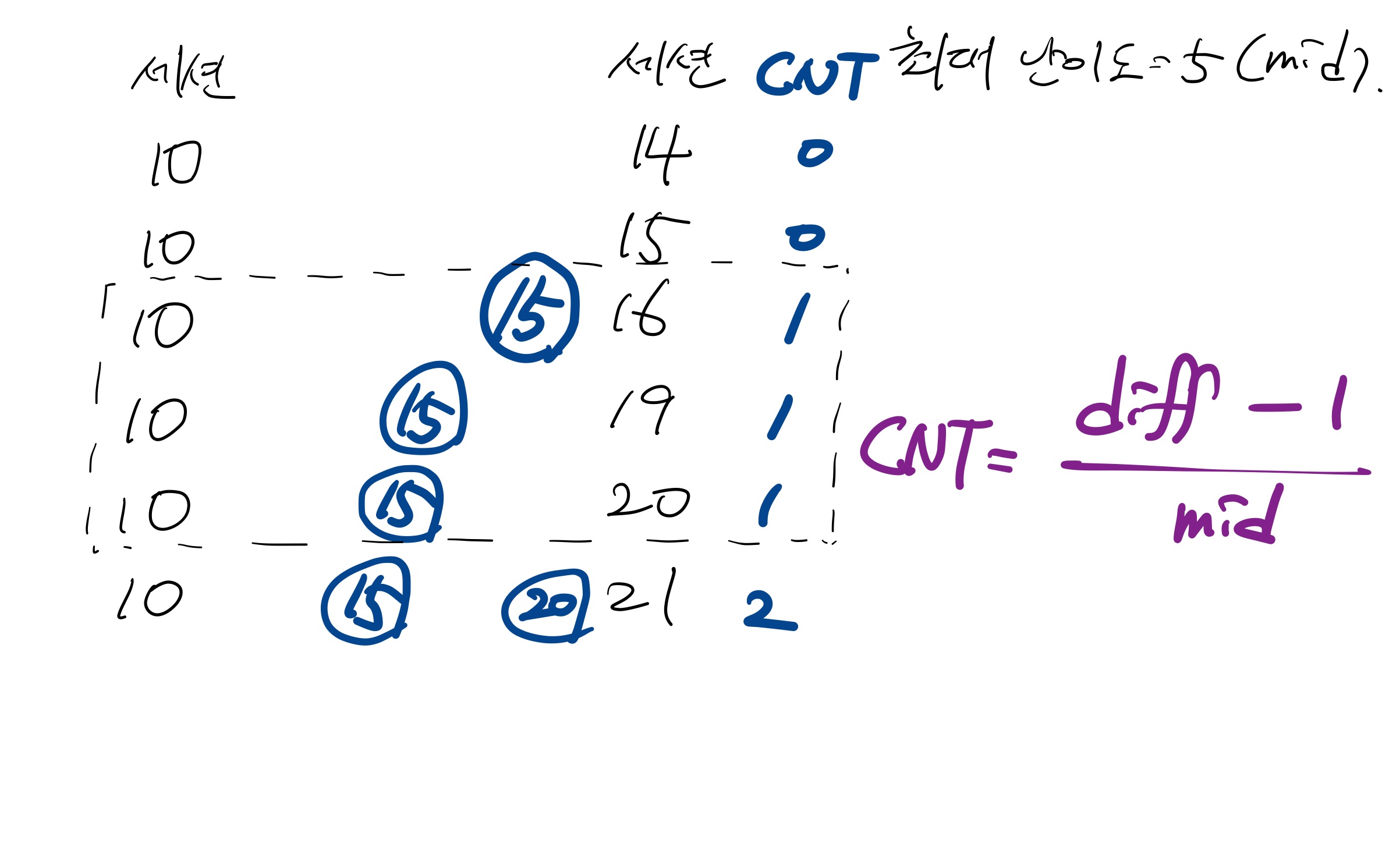
내가 헷갈렸던 부분이 이 부분이었는데, 만약 mid값이 5로 정해질 경우 cnt를 세 줄때 두 세션간 차이를 diff 라고 하면 위의 그림처럼 (diff-1)/mid 값을 계산해서 더해 주어야 하며 이 값이 음수가 나오면 안된다. 여기서 -1을 안 해주어서 계속해서 엣지 케이스를 처리를 못 해주었고 이 부분에서 개인적으로 시간을 많이 잡아먹었던 것 같다. 이렇게 풀게 되면 시간 복잡도는 O(N)이 나오게 된다.
4번 문제는 이번에는 못 풀었지만 나중에 기회가 되면 꼭 풀어보려고 한다. 킥스타트 문제가 되게 좋다. 많이 풀어보는 것을 추천!
'Computer Sci. > Algorithms' 카테고리의 다른 글
| [킥스타트] Google Kick Start 2020 Round C 문제 풀이 (0) | 2020.12.22 |
|---|---|
| [킥스타트] Google Kick Start 2020 Round B 문제 풀이 (1) | 2020.12.03 |
| 백준 3012 / 올바른 괄호 문자열 / DP, 분할 탐색 / JAVA / 플레티넘 3 (0) | 2020.09.15 |
| 백준 2146 / 다리 만들기 / BFS / JAVA / 골드 3 (0) | 2020.09.08 |
| 백준 1701 / Cubeditor / 문자열, KMP / JAVA (1) | 2020.08.14 |
