이번에 살펴볼 문제는 백준 1507번 궁금한 민호 문제이다.
https://www.acmicpc.net/problem/1507
1507번: 궁금한 민호
강호는 N개의 도시로 이루어진 나라에 살고 있다. 각 도시는 M개의 도로로 연결되어 있으며, 각 도로를 지날 때 필요한 시간이 존재한다. 도로는 잘 연결되어 있기 때문에, 도시 A에서 B로 이동할
www.acmicpc.net

이 문제는 플로이드 와셜 알고리즘을 통해 모든 경로를 탐색하여 푸는 문제이다. 모든 쌍의 최단 경로를 다 확인하는 문제로 이 알고리즘이 익숙하지 않으면 조금 생각하기 어려울 수도 있다. 먼저 플로이드 와셜 알고리즘에 대해 간단하게 설명한 후에 문제를 풀어 보도록 하겠다.
플로이드 와셜 알고리즘(Floyd Warshall Algorithm)은 모든 쌍의 최단 경로를 탐색하는 알고리즘 중 하나이다. N개의 노드로 이루어진 그래프가 있을 때 임의의 두 노드를 선택해서 두 노드간의 최단 경로를 알 수 있게 만드는 것이 목표이다. 임의의 두 노드(Vi, Vj)가 주어졌을 때 그 중간 지점들의 집합을 { v1, v2, ... , vk } 처럼 k개의 노드로 이루어져 있다고 할 때, i 부터 j 까지의 최단 경로는 다음과 같이 구할 수 있다.
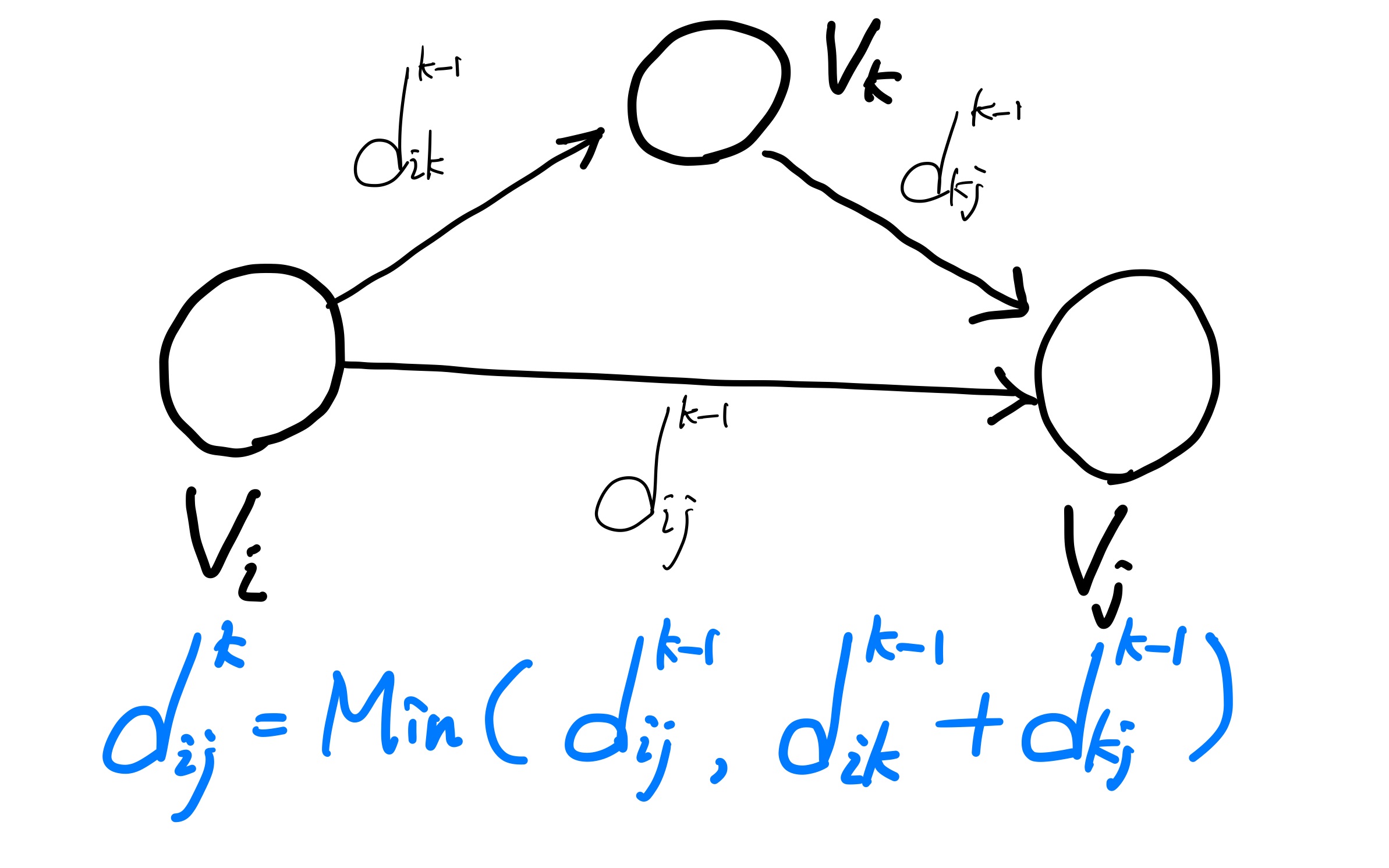
여기서 vi -> vj를 가는 거리와 vi -> vk -> vj를 가는 거리를 비교하는 식으로 모든 중간 지점 { v1. v2. ..., vk }에 대해서 비교하면 vi -> vj의 최단 거리를 찾을 수 있다.
이 연산을 1, 2, ... ,N 까지의 i와 1, 2, ..., N까지의 j에 대해서 수행하면 모든 노드에 대해 임의의 두 노드 사이의 최단 거리를 구할 수 있다.

위의 의사코드에서 알 수 있듯이 플로이드 와셜 알고리즘의 시간복잡도는 O(N^3)이다.
이제 문제를 풀어보자. 문제에서는 모든 도시간 최단 거리가 입력값으로 주어지고, 이 조건을 만족하는 가장 적은 도로의 갯수일 때 모든 도로의 가중치 값을 구하라고 했다. 그래서 우리는 다음과 같은 생각을 해볼 수 있다.
플로이드 와셜 알고리즘을 통해 모든 쌍에 대해서 중간지점을 거쳐가는 경우를 비교해 볼 수 있는데, 케이스를 다음과 같이 세 가지로 나누어서 생각할 수 있다. 중간지점을 거쳐 가는게 더 가중치가 크거나, 같거나, 더 작거나.
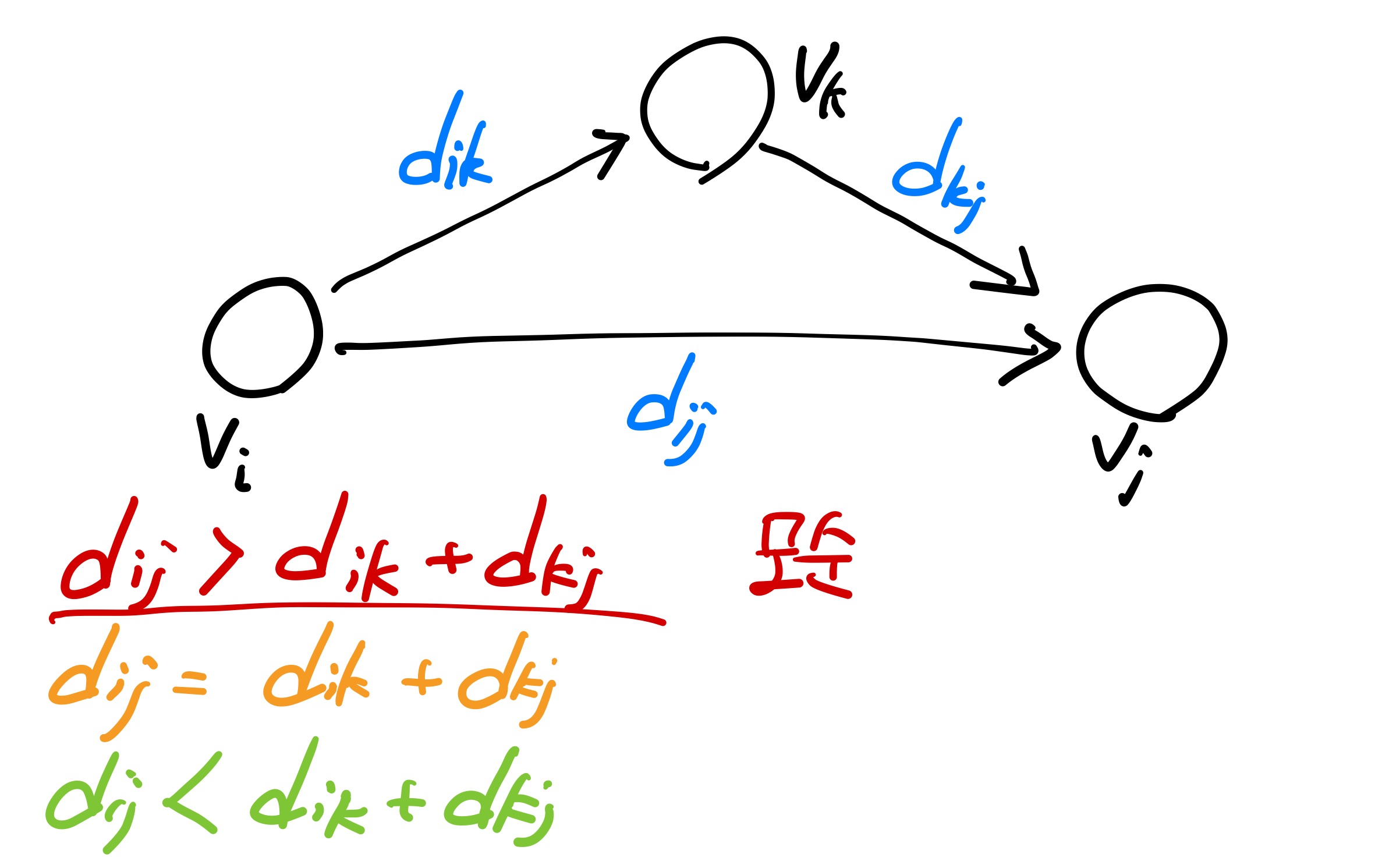
첫 번째로 가중치가 직접 가는게 더 큰 경우는.. 결론부터 말하면 모순이다. 왜냐하면, 문제에서 주어진 입력값은 두 노드 사이의 최단 거리라고 했는데 중간지점을 거쳐 가는게 더 가중치가 작다는 말은 이미 직접 Vi에서 Vj로 가는게 최단 거리가 아니라는 의미이기 때문이다. 따라서 이러한 경우가 발견되면 -1을 리턴해야 한다.
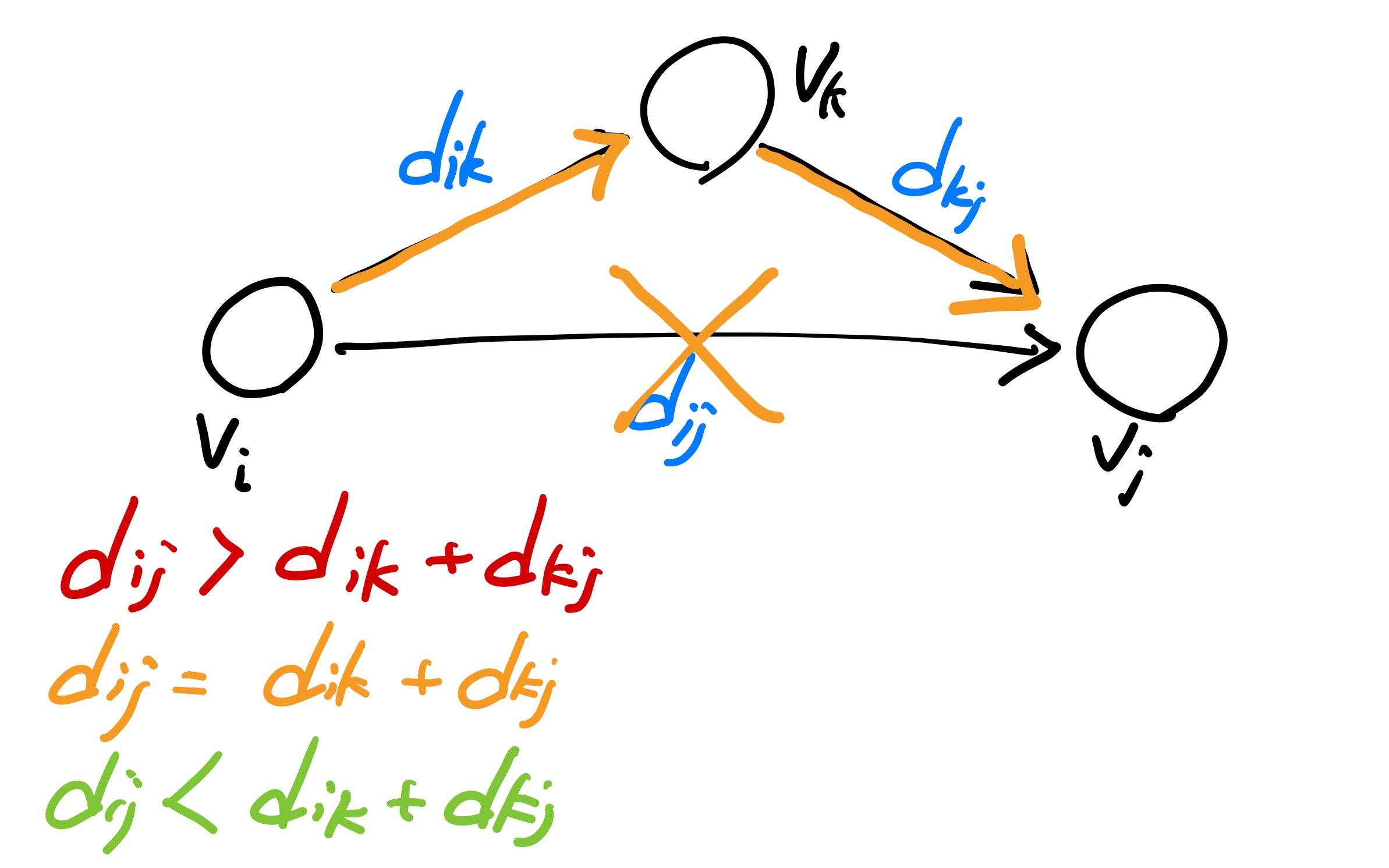
두 번째로 가중치가 같은 경우는 Vi->Vk->Vj와 Vi->Vj가 가중치가 같다는 의미이므로 Vi->Vj는 지워줄 수 있다. 문제에서 존재할 수 있는 도로의 최솟값을 구하라고 하였고, 여기서 Vi->Vj가 없어도 이 가중치는 변함이 없기 때문이다.

마지막으로 가중치가 직접 가는게 더 작은 경우는 모든 경로를 살려 둔다. 모두 다 필요하기 때문이다.
이런 처리를 하면서 지워줄 수 있는 간선을 체크하기 위해 모든 간선에 대해 boolean 이차원 배열인 canErased를 하나 설정했다. 이 배열에서 지워줄 수 있는 값을 true로 바꿔주고 마지막에 계산할 때 이 값이 false인, 즉 반드시 필요한 간선들만 가중치를 더해서 결과를 출력하는 식으로 문제를 해결했다.

내가 제출한 자바 소스코드는 다음과 같다.
이 문제를 통해 헷갈렸던 플로이드 와셜 알고리즘에 대한 개념을 다시 한 번 잡게 되었다. 그래프 유형의 문제로 꼭 풀어보기를 바라는 좋은 문제이다.
'Computer Sci. > Algorithms' 카테고리의 다른 글
| 백준 1701 / Cubeditor / 문자열, KMP / JAVA (1) | 2020.08.14 |
|---|---|
| 백준 1202 / 보석 도둑 / 그리디, 우선순위 큐 / JAVA (0) | 2020.07.06 |
| 백준 2352 / LIS(최장 증가 수열), DP / JAVA (0) | 2020.06.17 |
| 프로그래머스 종이접기 / 이진 트리, 순회 / JAVA (0) | 2020.06.03 |
| 백준 3176 / LCA 알고리즘, DP, DFS / JAVA (2) | 2020.05.20 |
